Eva Weißmüller 29.3.2005 S22EmpirischesGesetz.mcd
Das Empirische Gesetz der großen Zahlen
Bei einer ausreichend großen Anzahl von Experimenten stabilisiert sich die relative Häufigkeit eines Ereignisses um einen festen Zahlenwert.
Bsp.:
Def.: Sei W ein Ergebnisraum, für den die Ergebnisalgebra gilt.
Eine Funktion P(E) heißt Wahrscheinlichkeitsmaß, wenn folgende Axiome gelten:
1.
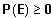für alle Ereignisse, die Teilmenge von W sind.
2.
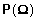= 1
3.
P(E1
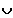E2) = P(E1) + P(E2) mit E1
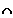E2 = { }
Man nennt diese Axiome auch "Kolmogorov-Axiome"
Folgerungen: Seien Elementarereignisse unvereinbar:
P(E) = P{w1} + P{w2} +...P{wm} für E = {w1}
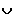{w2}
...
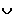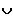{wm}
analog:
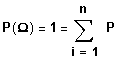({w1})
daraus: P(E)
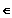[ 0 ; 1]
Da P(W) = P(W) + P({ }) = 1 gilt: P({ }) = 0
