Eva Weißmüller 29.3.2005 S324Permutationen.mcd

Permutationen

Eine Permutation von n Elementen ist jede Komplexion, in der alle n unterschiedlichen
Elemente in irgend einer Reihenfolge aufgezählt werden.

1. Volle Permutationen:

Gesucht ist die Anzahl P(n) der Permutationen aus der Menge A.
Jedes n-Tupel (a_1, a_2, a₃, ...,a_k) mit verschiedenen a_i 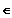A ist eine solche Permutation aus der Menge A.

Satz: P(n) = 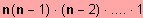= n!

(Ohne Wiederholung!)

Man spricht auch von einer n Fakultät. Verallgemeinert bedeutet n!, dass n unterschiedliche
Elemente auf n Plätze verteilt werden.

Bsp.: 3 Elemente a, b, c P(3) = 6
Permutationen: abc , acb , bac , bca , cab , cba

2. k-Permutationen

Gesucht ist die Anzahl aller geordneten Stichproben ohne Zurücklegen der Länge k,
bzw. die Anzahl P(n, k) der k-Permutationen aus der Menge A.
Jedes k-Tupel (a_1, a_2, a₃, ...,a_k) mit verschiedenen a_i 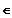A ist eine solche k-Permutation aus der
Menge A.

Bsp.: A = { 1 ; 2 ; 3 ; 4 } ; k = 2
1. Stelle: 4 Möglichkeiten 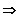4
2. Stelle: 3 Möglcihkeiten 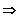3
Daraus ergeben sich 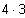= 12 Möglichkeiten

Allgemein: Eine Menge mit n Elementen
1. Stelle: n Möglichkeiten
2. Stelle: n 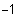Möglichkeiten
3. Stelle: n 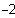Möglichkeiten
k. Stelle: n 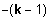Möglichkeiten
P(n; k) = =
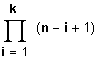
n. Stelle: 1 Möglichkeit
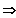n! Möglichkeiten

Satz: P(n, k) =

(Ohne Wiederholung!)

Man spricht auch von Variationen. Variation meint eine Permutation mit n - k nicht unterscheidbaren Elementen.

Anzahl der Permutationen von n Elementen, wobei je n_i untereinander gleich sind:

Satz: P( n; n_i) =

(Mit Wiederholung!)

Bsp.: 3 Elemente a, a, b 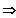P ( 3 ; 2 ; 1 ) = 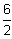= 3
Permutationen: aab, aba, baa

Impressum · Datenschutz