Eva Weißmüller 29.3.2005 S326n!UndBinomialkoeffizient.mcd

n!  (Fakultät)

Gesucht ist die Anzahl P(n) der Permutationen aus der Menge A.
Jedes n-Tupel (a_1, a_2, a₃, ...,a_k) mit verschiedenen a_i A ist eine solche Permutation aus der Menge A.

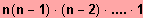Satz: P(n) = = n!

(Ohne Wiederholung!)

Man spricht auch von einer n Fakultät. Verallgemeinert bedeutet n!, dass n unterschiedliche
Elemente auf n Plätze verteilt werden.

Bsp.: 3 Elemente a, b, c 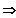P(3) = 6
Permutationen: abc , acb , bac , bca , cab , cba

Es sei 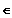n N:
n! =

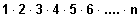
Wir legen fest: 0! = 1

Bsp.: 1! = 1 ; 2! = 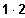; 3! = 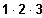; 4! = 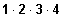; k! =

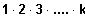
Binomialkoeffizient

Man spricht von Kombinationen, wenn die Reihenfolge der k Kandidaten, die aus
n Elementen ausgewählt werden, keine Rolle spielen.

1 für k = 0

("n über k")

=

{

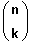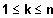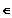für ; k,n N

  Im Nenner und Zähler stehen gleich viele Faktoren, nämlich k Faktoren.

  Zusätzlich ist festzustellen: 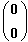= 1

Die Binomialkoeffizienten lassen sich ausschließlich durch Fakultäten darstellen:

= = =

Bsp.:

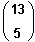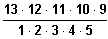= = 792

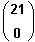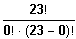= = 1

Kombinationen: 4 Elemente a, b, c, d ; k = 2 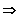Kombinationen ( 4 ; 2 ) = 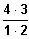= 6

Impressum · Datenschutz