Eva Weißmüller 29.3.2005 S430Bernoulli-Ketten.mcd
Bernoulli-Experimente
Def.: Ein Bernoulli-Experiment ist einZufallsexperiment, bei dem nur zwei Elementarereignisse möglich sind, sich der Ergebnisraum also in der Form
W = { T; N } darstellen lässt.
Dabei gilt: P(T) + P(N) =1, T und N stellen also Ereignis und Gegenereignis dar.
p0 = 1 ; q0 = 1 ;
p + q = 1
Bsp.: Kartenspiel: W = {rot ; schwarz}
Augenzahl: W = {gerade ; ungerade}
Elektrogerät: W = {funktioniert ; funktioniert nicht}
T = Treffer, N = Niete
Man spricht von einer Bernoulli-Kette der Länge n oder einem n-stufigen Bernoulli-Experiment, wenn man ein Bernoulli-Experiment mehrmals (n-mal) ausführt und damit einen neuen Ergebnisraum mit Tripeln, Paaren o.ä. erzeugt.
Ergebnisraum Wn = Wn = { T ; N}n
Def.: n gleiche Bernoulli heißen voneinander unabhängig, wenn gilt:
P´({(X1 ; X2 ; X3 ;...; Xn)}) = P({X1}) * P({X2}) * P({X3})* ....* P({Xn})
Ist dies nicht der Fall, heißen Bernpulli-Experimente voneinander abhängig.
Die Berechnung von Bernoulli-Ketten mit Hilfe des binmoischen Satzes
Satz: Bei einem Bernoulli-Experiment sei p
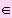] 0 ; 1[ die Wahrscheinlichkeit für einen Treffer.
Dann erzielt man bei der Durchführung einer Bernoulli-Kette der Länge n genau
k Treffer mit der Wahrscheinlichkeit:
B("genau k Treffer") = B(n ; p ; k) =
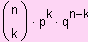mit p + q = 1
B(n ; p ; k) heißt "Wahrscheinlichkeit genau k Treffer zu erzielen bei einer
Bernoulli-Kette der Länge n mit der Trefferwahrscheinlichkeit p."
Bsp.: Urne mit weißen (=Treffer) und schwarzen (=Niete) Kugeln; 3 Züge mit Zurücklegen
Gesucht ist die Anzahl k der gezogenen weißen Kugeln (Wahrscheinlichkeit p für Treffer)
1. Ergebnis des Experiments: TTT
Wahrscheinlichkeit dieses Ergebnisses: ppp = p3
Anzahl der k Treffer: 3
zugeordnete Wahrscheinlichkeit B(k): p3
2. Ergebnis des Experiments: TTN TNT NTT
Wahrscheinlichkeit dieses Ergebnisses: ppq = p2q pqp = p2q qpp = p2q
Anzahl der k Treffer: 2 2 2
zugeordnete Wahrscheinlichkeit B(k): 3p2q
3. Ergebnis des Experiments: TNN NTN NNT
Wahrscheinlichkeit dieses Ergebnisses: pqq = pq2 qpq = pq2 qqp = pq2
Anzahl der k Treffer: 1 1 1
zugeordnete Wahrscheinlichkeit B(k): 3pq2 3pq2 3pq2
4. Ergebnis des Experiments: NNN
Wahrscheinlichkeit dieses Ergebnisses: qqq = q3
Anzahl der k Treffer: 0
zugeordnete Wahrscheinlichkeit B(k): q3
Die Wahrscheinlichkeiten erinnern an den binomischen Satz:
B( n ; p ; k) =
Binom. Satz:
