Eva Weißmüller 29.3.2005 S521Erwartungswert.mcd
Erwartungswert
Häufig interessiert man sich gar nicht so sehr für die Einzelheiten der Wahrscheinlichkeitsfunktion der Zufallsgröße ( Augensumme), sondern für den durchschnittlichen Wert, den die Zufallswerte
bei mehreren oder vielen Wiederholungen des Zufallsexperiments annehmen.
Dieser Mittelwert der Augensumme heißt Erwartungswert.
Def.: X sei eine Zufallsgröße, die ihre Werte x1, x2, x3, ...xn mit den Wahrscheinlichkeiten
W(x1), W(x2), W(x3), ...W(x4) annimmt.
 In diesem Fall heißt E(X) = x1 W(x1),+ x2W(x2) + x3W(x3) + ... + xnW(xn) =
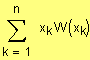
der Erwartungswert der Zufallsgröße X mit der Wahrscheinlichkeitsfunktion W.
Bsp.: Bei n Würfen tritt der Zufallswert x = 2 theoretisch 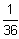-mal auf.
 x = erhält man demnach -mal, usw.
Die bei n Würfen insgesamt erzielte Augenzahl Z beträgt also:
Z = =
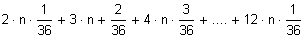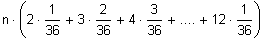
Der Erwartungswert beträgt dann 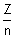. Der Erwartungswert wird mit den griechischen Buchstaben m
oder mit E(X) bezeichnet.
m = = =
Der Erwartungswert m ist unabhängig von der Anzahl der Versuche.
 Je größer die Zahl der Versuche ist, desto genauer wird der Erwartungswert.
Impressum · Datenschutz