Eva
Weißmüller
29.3.2005 S522Varianz.mcd
Varianz
Bsp.: Man betrachte zwei unterschiedliche
Zufallsgrößen X1 und X2
mit den dazugehörigen Wahrscheinlichkeitsfunktionen W1
und W2.
x1
-1 0
1
2 3 4
sonstige
W(x1)
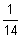
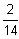
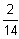
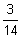
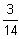
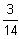 0
0
x2
-1
0 4 5 6 sonstige
W(x2)
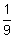
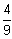
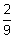
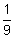
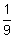 0
0
m1 =
m2
= 2
Der Erwartungswert allein reicht für eine
Charakterisierung der Wahrscheinlichkeitsfunktion nicht aus.
Es wird ein Maß benötigt, wie weit die
Zufallswerte um ihren Erwartungswert nach rechts und links (Graph)
streuen. Dieses Maß liefert für X1 einen
kleineren Wert als X2.
Man kann zur Definition des gesuchten Maßes
die durchschnittliche Abweichung der Zufallswerte xk
von ihrem Erwartungswert m
betrachten.
Def.: X sei eine
Zufallsgröße, die ihre Werte x1, x2, x3, ..., xn
mit den Wahrscheinlichkeiten,
W(x1), W(x2),
W(x3), ..., W(xn)
annimmt.
Die Varianz
mit der
Zufallsgröße X mit der Wahrscheinlichkeitsfunktion W
heißt dann:
Var(X) =
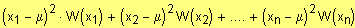 =
=
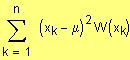
Oft schreibt man für Var(X) auch s2.
Die Varianz als Maß für die Streuung
hat auch Nachteile, da sie die Streuung nicht in der Einheit der
Zufallswerte mißt. Ist der Zufallswert beispielsweise ein
Euro-Betrag ergibt sich für die Varianz die Einheit ( € )2.
Eine andere Größe ist die
Standardabweichung (siehe "5.2.3 Standardabweichung").