Abschlussprüfung
1998 zum Erwerb der Fachhochschulreife an Berufsoberschulen
Mathematik
(nichttechnische Ausbildungsrichtungen)
(Arbeitszeit für
eine A- und eine S-Aufgabe insgesamt 180 Minuten)
Aufgabengruppe A
A I
1.0
Gegeben sind die reellen Funktionen
fk:
x 
fk (x);
Df k =IR , fk(x)
= (x-4)2(x + k) mit k 
IR.
Der
Graph einer solchen Funktion fk in einem kartesischen
Koordinatensystem heißt Gfk.
1.1 Für einen geeigneten Wert des Parameters k
hat die zugehörige Funktion fk eine Stammfunktion F, deren Graph GF
im Koordinatenursprung einen Wendepunkt besitzt. Bestimmen Sie diesen Wert des Parameters k
und den Funktionsterm F(x) der Stammfunktion F. (8BE)
Für
alle folgenden Teilaufgaben sei k =2. Zur Funktion f2 gehört der
Funktionsterm
f2
(x) = 
( x - 4 )2(x
+ 2) bzw. f2(x) = 
.
1.2
Geben Sie die Nullstellen der Funktion f2 an
und ermitteln Sie für den Graphen Gf2 Art und Koordinaten der
relativen Extrempunkte sowie die Koordinaten des Wendepunktes.
(10BE)
1.3 Zeichnen Sie den Graphen Gf2 mit
Hilfe bisheriger Ergebnisse und einer geeigneten Wertetabelle für -2,5
x 6 auf ein gesondertes DIN-A4-Blatt. (6BE)
Maßstab
auf beiden Achsen: 1 LE = 1 cm.
1.4.0 Die Funktion
f2´ ist die 1. Ableitungsfunktion der Funktion f2.
Der Graph dieser Ablei-tungsfunktion f2´ wird mit Gf2´ bezeichnet.
1.4.1 Zeichnen Sie in das vorhandene
Koordinatensystem für -2 x 6 den Graphen Gf2´
ein.
(3BE)
1.4.2 Berechnen Sie die Abszissen der Schnittpunkte
der Graphen Gf2 und Gf2´. (7BE)
1.4.3 Die y-Achse und die Graphen Gf2 und
Gf2´ begrenzen im I. und IV. Quadranten des Koordinatensystems ein
Flächenstück. Markieren Sie dieses Flächenstück in der vorhan-denen Zeichnung
und berechnen Sie die Maßzahl seines Flächeninhalts. (6BE)
1.5
Geben Sie unter Verwendung der vorhandenen Graphen die
maximalen Monotonie-intervalle der Stammfunktionen FC der Funktion f2
sowie Art und Abszisse des relativen Extremums einer solchen Stammfunktion FC
an. (3BE)
Fortsetzung siehe
nächste Seite
Fortsetzung A I
1.6.0 Gegeben ist nun die reelle Funktion 
; Dg = IR\{-2}.
1.6.1 Berechnen Sie den Grenzwert a = 
.
Bestimmen sie diejenigen x-Werte mit x
Dg, für
die gilt: |g(x)-a|<
. (5BE)
1.6.2 Welcher mathematische Zusammenhang besteht
zwischen der Funktion g und der 2.Ablei-tungsfunktion f2´´ der
Funktion f2 (siehe 1.2)? Die Antwort ist genau zu begründen.(3BE)
2 Ein allseits geschlossener Quader mit
quadratischer Grundfläche der Seitenlänge a und mit der Höhe h soll ein Volumen
von 100 cm3 besitzen. Die von
a abhängige Maßzahl der Oberfläche dieses Quaders wird mit S(a)
bezeichnet. Berechnen Sie a so, dass die
Größe S(a) ihren absolut kleinsten Wert annimmt. Weisen Sie die Art des Extremums ohne
Verwendung der 2. Ableitung der Funktion S nach. (9BE)
(Teilergebnis: Verwenden Sie für S(a)
die Form S(a) = 2a2 + 400
.)
Summe: 60 BE
A
II
1.0 Gegeben sind die reellen Funktionen
fk:
; Dfk =
IR , fk(x) = 
(x4 - kx2 -9x2 + 9 k)
mit k > 0 /\ k IR.
Der Graph einer solchen Funktion fk
in einem kartesischen Koordinatensystem heißt Gfk.
1.1.1 Untersuchen Sie den Graphen Gfk in
Bezug auf Symmetrie. (2BE)
1.1.2 Zeigen Sie, dass sich der Funktionsterm fk(x)
auch in der Form fk(x) = 
(x2 - k)(x2 - 9) schreiben lässt,
und ermitteln Sie Anzahl, Lage und Vielfachheit aller Nullstellen der Funktion
fk in Abhängigkeit von k. (9BE)
1.1.3 Berechnen Sie k so, dass die Tangente an den
Graphen Gfk an der Stelle xo = 1,5 parallel zur Geraden mit der Gleichung y = - 
x verläuft. (4BE)
1.2.0 Setzen Sie für die folgenden Teilaufgaben k
= 9.
1.2.1 Begründen Sie, dass für alle x 
IR gilt: f9(x)
> 0. Was kann daraus über die Lage des Graphen Gf9 im
Koordinatensystem gefolgert werden? (3BE)
Für
die folgenden Berechnungen sollte der Funktionsterm der Funktion f9
in der Form f9(x)=
verwendet werden.
1.2.2 Ermitteln Sie für den Graphen Gf9 Art und Koordinaten
aller relativen Extrempunkte sowie die Koordinaten der Wendepunkte. (11BE)
1.2.3 Zeichnen Sie den Graphen Gf9 mit Hilfe bisheriger Ergebnisse und einer geeigneten
Werte-tabelle für |x| 4. Verwenden Sie ein gesondertes
DIN-A4-Blatt im Hochformat mit dem Koordinatenursprung in der Blattmitte.
Maßstab auf beiden Achsen: 1 LE = 1cm. (6BE)
1.3.0 Die Parabel Gp ist der Graph der
quadratischen Funktion p : x p (x) ; Dp = IR.
Diese Parabel verläuft symmetrisch zur
y-Achse, schneidet die x-Achse im Punkt N(3; 0) und die Ordinate ihres
Scheitelpunktes hat den Wert yS = -3.
1.3.1 Bestimmen Sie den Funktionsterm p(x) und
zeichnen Sie die Parabel Gp im Bereich |x| < 4 in das
unter Teilaufgabe 1.2.3 beschriebene Koordinatensystem ein. (5BE)
(Teilergebnis: p (x) = 
x2 – 3)
1.3.2 Die Graphen Gf9 und Gp
schließen drei endliche Flächenstücke ein. Berechnen Sie für jenes
Flächenstück, das den Koordinatenursprung enthält, die Maßzahl seines
Flächeninhalts. (6BE)
1.4.0 Die Funktion F ist diejenige Stammfunktion der
Funktion f9 mit DF = IR, deren Graph GF den
Punkt A(-3; 0) enthält.
1.4.1 Bestimmen Sie den Funktionsterm F(x). (3BE)
1.4.2 Zeigen Sie unter Verwendung bereits
vorhandener Ergebnisse ohne weitere Rechnung, dass der Graph GF für
alle x IR echt monoton
steigt. Begründen Sie auch, dass dieser Graph genau zwei Terrassenpunkte
enthält. (5BE)
Fortsetzung siehe
nächste Seite
Fortsetzung A II
2
Gegeben ist nun die reelle Funktion g: x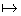 g (x) = 
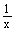; Dg = IR \{0}.
Bestimmen Sie unter Verwendung des
Differenzenquotienten die Ableitung der Funktion g an der festen, aber
beliebigen Stelle xo Dg .
Was lässt sich aus der Tatsache ihrer
Differenzierbarkeit in Bezug auf Stetigkeit bzw. Unstetigkeit der Funktion g an
der Stelle xo folgern? Die
Antwort ist ausführlich zu begründen. (6BE)
Summe: 60 BE
Aufgabengruppe
S
Stochastik
S I
Im Rahmen einer statistischen Erhebung
wurden 5000 repräsentative Haushalte ausgewählt und im Hinblick auf ihre
Ausstattung mit Fernsehern, Radiorecordern sowie Homecomputern untersucht.
Dabei gaben 4500 Haushalte an, einen (oder mehr) Fernseher zu besitzen, 4000
Haushalte verfügten über einen (oder mehr) Radiorecorder, aber 3500 Haushalte
besaßen keinen Homecomputer. Genau 1200 der Haushalte konnten sowohl
Radiorecorder als auch Homecomputer aufweisen. Die daraus ermittelten relativen
Häu-figkeiten werden als Wahrscheinlichkeiten interpretiert.
1.0 Für das Zufallsexperiment: "Zufällige Auswahl eines Haushalts, werden folgende Ereig-nisse betrachtet:
F: “Der
Haushalt besitzt einen (oder mehr) Fernseher.”
R: “Im
Haushalt gibt es einen (oder mehr) Radiorecorder.”
: “Der Haushalt
besitzt keinen Homecomputer.”
1.1 Zeigen Sie, dass die Ereignisse R und C
vereinbar sowie stochastisch unabhängig sind.(6BE)
Im Folgenden wird für alle drei Ereignisse F, R und C stochastische Unabhängigkeit vorausgesetzt.
1.2 Berechnen
Sie, mit welcher Wahrscheinlichkeit ein Haushalt sowohl mit Fernseher als auch
mit Homecomputer ausgestattet ist. (2BE)
1.3 Bestimmen
Sie für einen zufällig ausgewählten Haushalt mit Hilfe eines Baumdiagramms alle
möglichen Ausstattungsvarianten in Bezug auf die drei Gerätetypen. Ermitteln
Sie für dieses Zufallsexperiment auch die Wahrscheinlichkeiten aller denkbaren
Elementarereig-nisse. (6BE)
1.4 Berechnen Sie jeweils die
Wahrscheinlichkeit dafür, dass ein Haushalt
a) mindestens
zwei der drei Gerätetypen besitzt;
b) höchstens
einen der drei Gerätetypen besitzt;
c) Fernseher
oder Radiorecorder oder beides besitzt. (6BE)
2 Die Wahrscheinlichkeit, dass ein Haushalt
mit Homecomputer ausgestattet ist, beträgt weiterhin p = 0,3. Berechnen Sie die Wahrscheinlichkeiten für
folgende Ereignisse:
E1: "Von acht zufällig ausgewählten Haushalten besitzen nur genau
die beiden letzten Homecomputer."
E2: “Von acht zufällig ausgewählten Haushalten sind höchstens zwei der
drei zuletzt ausgewählten Haushalte mit Homecomputer ausgestattet, alle anderen
jedoch nicht.”
E3: “Von 20 zufällig ausgewählten Haushalten besitzen höchstens fünf Haushalte
Homecomputer.”
E4: “Von 50 zufällig ausgewählten Haushalten
besitzen mindestens 10 und höchstens 18 Homecomputer.” (9BE)
Fortsetzung siehe
nächste Seite
Fortsetzung S I
3.0 Eine Zusatzbefragung betraf die Anzahl der
pro Haushalt vorhandenen Radiorecorder. Keiner der Haushalte besaß mehr als
vier Radiorecorder. Die Zufallsgröße X gibt die Anzahl der Radiorecorder in
einem zufällig ausgewählten Haushalt an. Die Wahrschein-lichkeitsverteilung der
Zufallsgröße X lässt sich mit Hilfe der Parameter a, b, c IR wie folgt
darstellen:
x 0 1 2 3 4
P(X = x) 0,
2 a b c 0,05
Außerdem gilt: P(X < 2) =
0,55 sowie P(X 
2)= 0,70.
3.1 Berechnen
Sie a, b und c. Stellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße
X in Form eines Histogramms dar. (7BE)
(Teilergebnis: a = 0,1; b = 0,25)
3.2
Berechnen Sie die Standardabweichung der Zufallsgröße X. (4BE)
Summe: 40 BE
S
II
Für
ein Zufallsexperiment wird ein Spielbrett mit roten (R) grünen (G) und blauen
(B) Feldern verwendet (siehe Zeichnung).
Start G B R G B R
Ferner
steht je ein roter, grüner und blauer idealer Würfel zur Verfügung. Der rote
Würfel trägt auf einer Seitenfläche die 1, auf zwei Seiten die 2 und
auf drei Seiten die 3. Der grüne Würfel weist jede der drei Zahlen 1,
2 bzw. 3 mit gleicher Häufigkeit auf. Beim blauen Würfel kommt
die 2 auf zwei Seitenflächen, die 3 auf vier Seiten vor.
Der
Ablauf eines Spiels geht folgendermaßen vor sich:
Zu
Beginn wird eine Spielfigur auf das Startfeld gestellt und der rote Würfel
geworfen. Die Spielfigur wird um so viele Felder, wie die gewürfelte Augenzahl
angibt, weitergezogen. Die Farbe des
Feldes, auf dem die Spielfigur nun steht, bestimmt die Farbe des Würfels, mit
dem der zweite Wurf erfolgt. Anschließend wird die Spielfigur um die dem
zweiten Wurf entsprechende Felderzahl nach rechts gezogen. Damit endet das
Spiel.
1 Zeichnen Sie für das vorliegende Spiel
mit 
GB,GR,...,RR} ein Baumdiagramm. Berechnen Sie auch die
Wahrscheinlichkeiten sämtlicher Elementarereignisse. (6BE)
2.0 Als Treffer wird nun gewertet, wenn die
Spielfigur am Ende eines Spiels auf einem grünen Feld steht.
2.1 Zeigen
Sie: Die Trefferwahrscheinlichkeit beträgt p = 0,25. (2BE)
2.2 Die Zufallsgröße X gibt die Anzahl der
Treffer bei fünfmaliger Durchführung des Spiels an.
Stellen Sie die Wahrscheinlichkeitsverteilung der
Zufallsgröße X in Form eines Histo-gramms dar. Berechnen Sie den Erwartungswert
und die
Standardabweichung 
der Zufallsgröße X
und schraffieren Sie im Histogramm die Fläche mit der Flächenmaßzahl P(| X - | 
). (7BE)
2.3 Es werden nun folgende Ereignisse
betrachtet:
E1: “Bei 50-maliger Durchführung des Spiels werden mindestens 10
Treffer erzielt."
E2: “Bei 50-maliger Durchführung des Spiels
werden bei weniger als einem Viertel der
Spiele Treffer erzielt."
Berechnen
Sie die Wahrscheinlichkeiten der Ereignisse E1 und E2.
Untersuchen Sie auch, ob die beiden Ereignisse stochastisch unabhängig sind. (7BE)
Fortsetzung siehe
nächste Seite
Fortsetzung S
II
2.4 Bestimmen Sie für die Ereignisse aus
Aufgabe 2.3 folgende Wahrscheinlichkeiten:
a) P (E1 
E2) b) P(E1 
). (6BE)
3 Nach
etlichen Spielen entsteht der Verdacht, dass der rote Würfel häufiger als
erwartet eine 1 zeigt (Gegenhypothese). Zur Überprüfung wird ein
Signifikanztest der Länge 100 mit dem roten Würfel durchgeführt. Geben Sie die
Testgröße sowie die Art des Signifi-kanztests an und ermitteln Sie den
größtmöglichen Ablehnungsbereich der Nullhypothese bei einem Signifikanzniveau
von 1 %. (6BE)
4.0 Bei einem zweiten Signifikanztest erklärt
sich ein Spieler bereit, den roten Würfel als gut anzuerkennen, wenn bei
50-maligem Würfeln höchstens 10-mal die 1 erscheint.
4.1 Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Spieler bei diesem Signifikanztest den Würfel als “gezinkt" ablehnt, obwohl er in Wirklichkeit “gut" ist. (4BE)
4.2 Erklären Sie mit eigenen Worten, worin bei diesem Test der Fehler 2. Art besteht. (2BE)
Summe: 40 BE