Abschlussprüfung 1998 zum Erwerb der Fachhochschulreife an Berufsoberschulen

Mathematik BOS 12 (Ausbildungsrichtung Technik

(Arbeitszeit für eine A und eine B-Aufgabe insgesamt 180 Minuten)

Aufgabengruppe A

A I

Gegeben sind die reellen Funktionen

f_k : x e^kx·(kx - 2) mit k IR und k > 0

in der von k unabhängigen Definitionsmenge D = IR. Der Graph einer solchen Funktion f_k in einem kartesischen Koordinatensystem wird mit G_k bezeichnet.

1.1 Berechnen Sie die Nullstelle der Funktion f_k, und geben Sie die Bereiche an, in denen die Funktionswerte der Funktion f_k positiv bzw. negativ sind. (4 BE)

1.2 Untersuchen Sie das Verhalten der Funktionswerte f_k(x) für x und für x. (5 BE)

1.3 Untersuchen Sie das Monotonieverhalten der Funktion f_k. Bestimmen Sie damit Koordinaten und Art des Extremalpunktes des Graphen G_k, und zeigen Sie, dass die Extremalpunkte aller Graphen G_k auf einer zur x-Achse parallelen Geraden liegen. (7 BE)

(Teilergebnis: f_k'(x) = k·e^kx·(kx - 1) )

1.4 Untersuchen Sie das Krümmungsverhalten des Graphen G_k, und zeigen Sie, dass die Koordinaten des Wendepunktes des Graphen G_k von k unabhängig sind. (7 BE)

1.5 Ermitteln Sie eine Gleichung der Wendetangente t_k des Graphen G_k, und berechnen Sie, für welchen Wert des Parameters k die Wendetangente t_k parallel zur Geraden mit der Gleichung y = -x verläuft. (7 BE)

2.0 Setzen Sie nun für alle weiteren Teilaufgaben k = 1.

Die zugehörige Funktion f₁ besitzt die Funktionsgleichung f₁(x) = e^x·(x - 2) mit xIR.

2.1 Zeichnen Sie den Graphen G₁ der Funktion f₁ für x [-4; 2,2]. Verwenden Sie dazu bereits vorliegende Ergebnisse, und erstellen Sie für die Funktion f₁ eine Wertetabelle für ganzzahlige x-Werte. Berechnen Sie zusätzlich den Funktionswert f₁(2,2). Verwenden Sie eine eigene Seite im Querformat mit dem Koordinatenursprung in der Seitenmitte.

Maßstab auf beiden Achsen: 1LE = 2cm. (6 BE)

2.2 Weisen Sie nach, dass der Graph G₁ im Intervall [0; 1] an mindestens einer Stelle die Steigung m= - besitzt, ohne diese Stelle zu berechnen. (4 BE)

Fortsetzung siehe nächste Seite

Fortsetzung A I

2.3 Zeigen Sie, dass die Funktion F₁:x e^x·(x - 3) mit xIR eine Stammfunktion der Funktion f₁ ist, und bestimmen Sie nur mit Hilfe bereits vorliegender Ergebnisse die Abszisse und die Art des Extremwertes der Funktion F₁. (6 BE)

3.0 Gegeben sind nun noch die Funktionen g_a,b:x a·cos(bx) mit a, bR\{0} in der von a und b unabhängigen Definitionsmenge D = IR.

3.1 Bestimmen Sie die Werte a und b so, dass der Graph H der zugehörigen Funktion g_a,b durch den Punkt W(0; -2) verläuft und die kleinste, positive Nullstelle der zugehörigen Funktion g_a,b mit der Nullstelle der Funktion f₁ übereinstimmt.

(Teilergebnis:a = -2; b = ) (3 BE)

3.2 Zeichnen Sie den Graphen H der in Teilaufgabe 3.1 ermittelten Funktion mit Hilfe einer Wertetabelle für ganzzahlige x-Werte im Bereich lxl 4 in das Schaubild von Teilaufgabe 2.1 ein. (4 BE)

3.3 Die Graphen H und G₁ begrenzen im 4.Quadranten des Koordinatensystems ein Flächenstück. Kennzeichnen Sie dieses Flächenstück in Ihrer Zeichnung, und berechnen Sie die Maßzahl seines Flächeninhalts. (6 BE)

Ein Sportplatz besteht aus einem rechteckigen Hauptfeld und zwei halbkreisförmigen Nebenfeldern (siehe Skizze). Der Umfang des gesamten Sportplatzes beträgt 400 Meter.

4.0

4.1 Stellen Sie die Flächenmaßzahl A des Hauptfeldes als Funktion des Radius r der Nebenfelder dar, und geben Sie den Definitionsbereich der Funktion A(r) an. (5 BE)

(Mögliches Teilergebnis: A(r) = -2r² + 400r )

4.2 Ermitteln Sie, für welchen Wert von r die Flächenmaßzahl A(r) den absolut größten Wert annimmt, und berechnen Sie für diesen Fall die Länge und Breite des Hauptfeldes. (5 BE)

Summe:66BE

A II

Gegeben sind die reellen Funktionen f_a: mit a IR und a >0 in der jeweils größtmöglichen Definitionsmenge IR\{-2a}. Der Graph einer solchen Funktion f_a in einem kartesischen Koordinatensystem wird mit K_a bezeichnet.

1.1 Ermitteln Sie die von a abhängige Nullstelle der Funktion f_a sowie die Intervalle, in denen gilt: f_a(x) > 0 (4BE)

1.2 Untersuchen Sie das Verhalten der Funktionswerte f_a(x) für x, für x und in der Umgebung der Definitionslücke. Geben Sie die Gleichungen der Asymptoten des Graphen K_aan. (5BE)

1.3 Untersuchen Sie das Monotonieverhalten der Funktion f_a, und zeigen Sie, dass die Funktion f_a keine Extremwerte besitzt. (4BE)

1.4 Zeichnen Sie den Graphen K₁ der Funktion f₁ (für a = 1) im Bereich –6 x 4. Erstellen Sie dazu eine Wertetabelle mit der Schrittweite x = 1, berechnen Sie zusätzlich die Funktionswerte f₁(-2,5) und f₁(-1,5), und tragen Sie auch die Asymptoten des Graphen K₁ in Ihre Zeichnung ein. (6BE)

Maßstab auf beiden Achsen: 1LE = 1cm.

2.0 Nun wird die reelle Funktion h: x ln( f(₁x) ) mit h(x) =

in der größtmöglichen Definitionsmenge D betrachtet. Der Graph der Funktion h in einem kartesischen Koordinatensystem wird mit G bezeichnet.

2.1 Geben Sie die Definitionsmenge D der Funktion h an, und ermitteln Sie die Nullstelle der Funktion h. (3BE)

2.2 Untersuchen Sie das Verhalten der Funktionswerte h(x) am Rand der Definitionsmenge D, und geben Sie die Gleichungen der Asymptoten des Graphen G an. (6BE)

2.3 Untersuchen Sie das Monotonieverhalten der Funktion h. (5BE)

(Mögliches Teilergebnis: h'(x) = )

2.4 Bestimmen Sie das Krümmungsverhalten des Graphen G. (4BE)

2.5 Zeichnen Sie für -6 x 4 den Graphen G der Funktion h und seine Asymptoten mit Farbe in das Schaubild von Teilaufgabe1.4 ein. Fertigen Sie dazu eine Wertetabelle mit der Schrittweite x = 1 an, berechnen Sie zusätzlich den Funktionswert h(-2,5), und verwenden Sie Ihre bisherigen Ergebnisse. (6BE)

Fortsetzung siehe nächste Seite

Fortsetzung A II

3.0 Mit den Funktionen f₁ und h wird nun für x > - 0,5 die neue Funktion d: x f₁(x) - h(x) gebildet.

3.1 Veranschaulichen Sie den Funktionswert d(0) mit Farbe in Ihrer Zeichnung, und untersuchen Sie, wie sich die Funktion d an den Grenzen ihres Definitionsbereichs verhält. (4BE)

3.2 Ermitteln Sie ohne Verwendung der 2.Ableitung das absolute Minimum der Funktion d. (6BE)

4.0 Gegeben ist nun die Funktion g: x mit x IR.

4.1 Begründen Sie, dass die Graphen der Funktionen g und h im Bereich x < -2 genau einen Punkt S gemeinsam haben. (4BE)

4.2 Bestimmen Sie näherungsweise die Koordinaten des Punktes S. Verwenden Sie zur Lösung der entstehenden Gleichung das Newton-Verfahren mit dem Startwert x = -2,5 und führen Sie zwei Näherungsschritte durch. Geben Sie damit die Koordinaten des Punktes S auf zwei Nachkommastellen gerundet an. (6BE)

4.3 Überprüfen Sie das Ergebnis von Teilaufgabe 4.2 durch eine Zeichnung. (3BE)

Summe: 66 BE

Aufgabengruppe B

B I

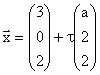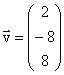In einem kartesischen Koordinatensystem sind die Punkte A(5; 10; 0), B(6; 9; -1) und C(3; 0; 2) sowie die Geraden h_a: mit , a IR und der Vektor gegeben.

1 Zeigen Sie, dass die Ortsvektoren der Punkte A, B und C eine Basis des IR³ bilden, und berechnen Sie die Komponenten des Vektors bezüglich dieser Basis. (8BE)

2 Die Punkte A und B bestimmen die Gerade g.

Geben Sie eine Gleichung der Geraden g an, und untersuchen Sie die Lagebeziehung zwischen der Geraden g und der Geraden h_a in Abhängigkeit von a.

Berechnen Sie dabei insbesondere, für welchen Wert des Parameters a die zugehörige Gerade h_a zur Geraden g parallel ist. (7BE)

3.0 In dieser Teilaufgabe ist a = -2.

3.1 Bestimmen Sie eine Gleichung der von den Geraden g und h_-2 aufgespannten Ebene E in Koordinatenform. (3BE)

(Ergebnis: E: x₁ + x₃ - 5 = 0 )

3.2 Ermitteln Sie eine Gleichung der Schnittgeraden der Ebene E mit der x₁ -x₃ -Ebene, und berechnen Sie den Winkel, den die Ebene E mit der x₂-x₃-Ebene einschließt. (5BE)

3.3 Veranschaulichen Sie die Lage der Ebene E im Koordinatensystem in einer geeigneten Skizze. (3BE)

4.0 Setzen Sie nun a = 1.

4.1 Die Lotgerade l steht senkrecht auf der Geraden h₁ und enthält den Punkt A(5; 10; 0) der Geraden g. Ermitteln Sie eine Gleichung der Lotgeraden l.(5BE)

4.2 Zeigen Sie, dass die Lotgerade l auch auf der Geraden g senkrecht steht, und berechnen Sie dann den Abstand der Geraden g und h₁. (3BE)

Summe: 34 BE

B II

In einem kartesischen Koordinatensystem sind die Geraden

h_a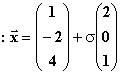 mit IR und g_a: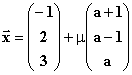mit IR und a IR gegeben.

1.1 Zeigen Sie, dass die Gerade h mit keiner der Geraden g_a einen Punkt gemeinsam hat. (4BE)

1.2 Vom Aufpunkt A(-1; 2; 3) der Geraden g_a wird das Lot auf die Gerade h gefällt.

Berechnen Sie die Koordinaten des Lotfußpunktes L, und ermitteln Sie den Abstand des Punktes A von der Geraden h. (5BE)

( Teilergebnis: L(-1; -2; 3) )

1.3 Bestimmen Sie den Wert des Parameters a so, dass die zugehörige Gerade g_a parallel zur Geraden h verläuft, und geben Sie für diesen Fall den Abstand der beiden Geraden an. (4BE)

1.4 Die beiden Geraden g₂ (für a = 2) und g₄ (für a = 4) spannen die Ebene E auf. Bestimmen Sie je eine Gleichung der Ebene E in Parameter- und Normalenform. (4BE)

( Teilergebnis: E: x₁+ x₂ - 2x₃ + 5 = 0 )

1.5 Zeigen Sie, dass alle Geraden g_a in der Ebene E liegen, und dass die Gerade h zur Ebene E parallel ist. (4BE)

1.6 Begründen Sie, dass für a 1 alle Geraden g_a windschief zur Geraden h sind, und zeigen Sie, dass der Abstand d zwischen der Geraden h und jeder solchen Geraden g_a d = beträgt. (5BE)

2.0 Die Punkte A(-1; 2; 3) und L(-1; -2; 3) aus Teilaufgabe 1.2 und der Aufpunkt H(1; -2; 4) der Geraden h sind die Eckpunkte des Dreiecks ALH.

2.1 Begründen Sie, dass das Dreieck ALH rechtwinklig ist, und berechnen Sie seine Flächenmaßzahl. (4BE)

2.2 Der Koordinatenursprung 0 ist die Spitze einer Pyramide mit dem Dreieck ALH als Grundfläche. Berechnen Sie die Maßzahlen des Volumens und der Höhe dieser Pyramide. (4BE)