GS - 20.05.06 - Skihang_anw_1.mcd
Abschnittsweise definierte Funktionen
- Aufgaben mit Anwendungsbezug -
Aufgabe 1:
Ein Skihang soll durch zwei quadratische Funktionen beschrieben werden:
Der Scheitel der nach unten geöffneten Parabel liegt bei (0 m ; 40 m), der Scheitel der nach
oben geöffneten Parabel liegt bei (100 m ; 0 m). Außerdem soll der Punkt (40 m ; 24 m) auf
beiden Parabeln liegen und die beiden Abschnitte trennen.
a) Geben Sie die Form des Hanges als abschnittsweise definierte Funktion an.
b) Bestimmen Sie die Tangente an beide Parabeln an der Übergangsstelle und den
Neigungswinkel des Hanges gegenüber der Meereshöhe.
c) Die prozentuale Steigung ist definiert als Höhenzunahme pro Längenzunahme.
12 % Steigung entspricht einer Höhenzunahme von 120 m pro 1000 m.
Das prozentuale Gefälle ist definiert als Höhenabnahme pro Längenzunahme.
10 % Gefälle entspricht einer Höhenabnahme von 100 m pro 1000 m.
Berechnen Sie das Gefälle des Skihanges.
Teilaufgabe a)
1. Parabel:
2. Parabel:
Gemeinsamer Punkt:
Einsetzen:
Funktionsterm:
Teilaufgabe b)
Ableitung:
Überprüfung der "Grenzwerte":
oder:
Die Funktion ist differenzierbar an der Nahtstelle
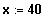, da ein Skihang "glatt" ist.
Steigung an der Übergangsstelle:
Tangente:
Neigungswinkel:
a
Teilaufgabe c)
Größte Steigung des Hanges hat die Tangente:
Höhenzunahme:
Längenzunahme:
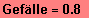entspricht 80 %
Aufgabe 2:
Der Querschnitt einer Skiflugschanze lässt sich durch abschnittsweise definierte Funktionen
bestimmen (die Maßeinheiten werden weggelassen):
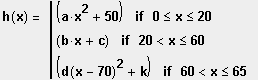
Die Punkte
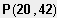und
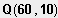liegen auf der Schanze, der Absprung vom
Schanzenzentisch in einer Höhe von 7 m entspricht dem Punkt
.
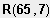a) Bestimmen Sie alle Koeffizienten so, dass keine Sprünge im Anlauf auftreten.
b) Welche Neigung hat das gerade Stück im Anlauf?
c) Berechnen Sie mithilfe der Steigung der Tangente den Absprungswinkel im
Absprungspunkt.
Teilfunktionen:
P
:
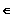
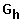Q
:
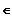
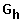Nahtstelle
:
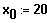Gleichungssystem:
Nahtstelle
:
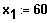R
:
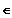
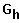Gleichungssystem:
Vereinfacht:
Konkrete Funktionsterme:
Schanzenquerschnitt:
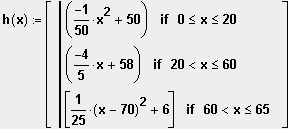
Teilaufgabe b)
Neigung des geraden Stückes:
Teilaufgabe c)
Absprungsfunktion:
Ableitung:
Steigung im Absprungpunkt:
Absprungwinkel:
