MK 2.6.2003 DiffbarkeitGrundlagen.mcd
Grundlagen der Differenzierbarkeit
Satz:
Ist eine Funktion an einer Stelle x0 differenzierbar, so ist sie an dieser Stelle auch stetig.
Die Umkehrung gilt nicht.
Bsp.:
Sei
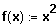 . Gesucht wird die Steigung im Punkt (3 / 9).
. Gesucht wird die Steigung im Punkt (3 / 9).
x0 = 3
LS
RS
Der Grenzwert existiert:
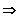 f ' (3) = 6
f ' (3) = 6
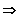 Die Steigung der Tangente an den Graphen von f im Punkt (3 / 9) ist 6
Die Steigung der Tangente an den Graphen von f im Punkt (3 / 9) ist 6
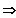 Die Steigung des Graphen von f im Punkt (3 / 9) ist 6
Die Steigung des Graphen von f im Punkt (3 / 9) ist 6
Bsp.:
Sei
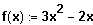 . Gesucht wird die Gleichung der Tangente im Punkt (1 / 1).
. Gesucht wird die Gleichung der Tangente im Punkt (1 / 1).
x0 = 1
LS
RS
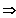 f ' (1) = 4
f ' (1) = 4
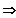 Tangente:
Tangente:
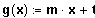
Bsp.:
Sei
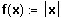 . Gesucht wird die Steigung im Punkt (0 / 0).
. Gesucht wird die Steigung im Punkt (0 / 0).
x0 = 0
LS
RS
Der Grenzwert existiert nicht:
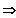 f ist an der Stelle (0 / 0) nicht differenzierbar.
f ist an der Stelle (0 / 0) nicht differenzierbar.
Satz:
Ist f (x) in D differenzierbar, so heißt f ' (x) Ableitungsfunktion von f (x).
Bsp.:
Sei
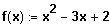 . D = R.
. D = R.
Wähle eine beliebige Stelle x0:
LS
=
RS
=
Der Grenzwert existiert:
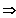 f ist an der Stelle x0 differenzierbar.
f ist an der Stelle x0 differenzierbar.
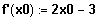
x0 ist beliebig.
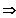 f besitzt eine Ableitungsfunktion.
f besitzt eine Ableitungsfunktion.