MK 2.6.2003
Differentiation_Ueb_2_Untersuch.mcd
Übung: Untersuchung einfacher Funktionen
Aufgaben:
Untersuchen Sie die folgenden zusammengesetzen
Funktion auf Differenzierbarkeit und Stetigkeit.
(1)
für
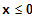
für
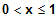
für
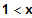
(2)
für
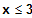
für
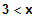
(3)
für
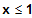
für
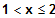
für
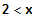
(4)
In welchem Punkt des Graphen von
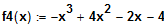verläuft eine Normale parallel zur Geraden
?
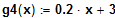(5)
Differenzieren Sie
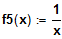und
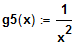. Welche Vermutung haben Sie bei
?
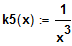(6)
Gegeben ist die Funktion
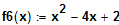. Welche beiden Tangenten schneiden sich unter einem
rechten Winkel und die Abszisse unter 45°?
(7)
Die Gerade
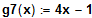ist Tangente an den Graphen von
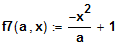Bestimmen Sie daraus den Parameter
.
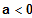Bestimmen Sie die Parameter in den folgenden
zusammengesetzen Funktionen so, dass die Funktionen überall stetig
und differenzierbar sind.
(8)
für
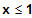
für
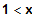
Geht über den LP
FOSBOS 2003 hinaus
(9)
für
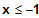
für
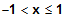
für
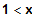
Lösungen:
Untersuchen Sie die folgenden zusammengesetzen
Funktion auf Differenzierbarkeit und Stetigkeit.
(1)
für
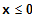
Alle Terme sind Polynome. Folglich sind alle Terme
in ihrem Definitionsbereich stetig und differenzierbar.
für
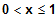
für
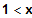
x0 = 0
LS
RS
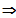Die Funktion ist differenzierbar an dieser Stelle
und somit auch stetig.
x0 = 1
LS
RS
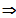Die Funktion ist differenzierbar an dieser Stelle
und somit auch stetig.
(2)
für
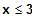
Alle Terme sind Polynome. Folglich sind alle Terme
in ihrem Definitionsbereich stetig und differenzierbar.
für
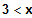
x0 = 3
LS
RS
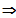Die Funktion ist differenzierbar an dieser Stelle
und somit auch stetig.
(3)
für
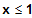
Schnittstelle bei 0 berücksichtigen!
für
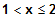
Alle Terme sind Polynome. Folglich sind alle Terme
in ihrem Definitionsbereich stetig und differenzierbar.
für
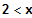
x0 = 0
für
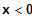
für
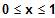
LS
RS
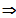Die Funktion ist nicht differenzierbar bei x0 = 0,
nun muss die Stetigkeit untersucht werden.
LS
RS
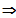Die Funktion ist stetig an dieser Stelle.
x0 = 1
LS
RS
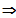Die Funktion ist differenzierbar an dieser Stelle
und somit auch stetig.
x0 = 2
LS
RS
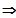Die Funktion ist nicht differenzierbar bei x0 = 2,
nun muss die Stetigkeit untersucht werden.
LS
RS
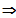Die Funktion ist nicht stetig an dieser Stelle.
(4)
In welchem Punkt des Graphen von
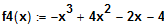verläuft eine Normale parallel zur Geraden
?
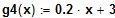Gehört nicht mehr zur Aufgabe:
(5)
Differenzieren Sie
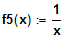und
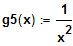. Welche Vermutung haben Sie bei
?
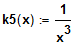f5(x), Stelle x0
LS unten, RS analog
g5(x), Stelle x0
LS unten, RS analog
Also:
und
lässt den Schluss zu
(6)
Gegeben ist die Funktion
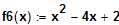. Welche beiden Tangenten schneiden sich unter einem
rechten Winkel und die Abszisse unter 45°?
(7)
Die Gerade
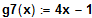ist Tangente an den Graphen von
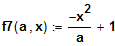Bestimmen Sie daraus den Parameter
.
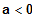(I)
(II)
Aus (II)
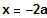in (I)
Bestimmen Sie die Parameter in den folgenden
zusammengesetzen Funktionen so, dass die Funktionen überall stetig
und differenzierbar sind.
(8)
für
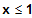
Alle Terme sind Polynome. Folglich sind alle Terme
in ihrem Definitionsbereich stetig und differenzierbar.
für
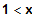
x0 = 1
LS
RS
nur diffbar, falls -4+c = 0
c = 4
=
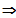Die Funktion ist für
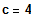differenzierbar an der Stelle x0 = 1 und somit auch
stetig.
(9)
für
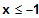
Alle Terme sind Polynome. Folglich sind alle Terme
in ihrem Definitionsbereich stetig und differenzierbar.
für
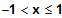
für
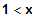
x0 = -1
LS
RS
nur diffbar, falls 1+d1 = 0
d1 = -1
=
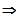Die Funktion ist für
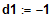differenzierbar an der Stelle x0 = -1 und somit
auch stetig.
x0 = 1
LS
RS
=
nur diffbar, falls 7-3d2+d3 = 0
falls 3 -3d2 = -6
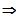Die Funktion ist für
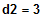und
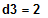differenzierbar an der Stelle x0 = 1 und somit auch
stetig.
