MK 18.10.2004 D3_GrenzwertSteigung.mcd
Der Grenzwert des Differenzenquotienten
Es soll die Steigung an der Stelle
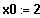des
Graphen der Funktion f mit der Gleichung bestimmt werden.
Probieren Sie es mit zwei Sekanten, bei denen ein
Punkt fix (bei x = 2) , der andere Punkt aber auf der Kurve
verschiebbar ist.
Man stellt fest, dass die Sekante verschwindet,
wenn die Stützpunkte der Sekante identisch sind.
Rechnen Sie nach:
Seien (px / py) und (qx / qy) die Koordinaten der
Punkte P und Q, und der Punkt S habe die Koordinaten (x0 / y).
Dann gelten für die Differenzenquotienten und
somit für die Steigungen der Sekanten:
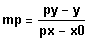und
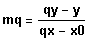
Falls die Punkte P und S oder Q und S identisch
sind, gilt auch px=x0 oder qx=x0 und der entsprechende
Differenzenquotient hat eine 0 im Nenner und ist damit nicht
definiert.
Wenn man die Sekantensteigung möglichst genau
haben will, nähert man die Werte px und x0 oder qx und x0 einander an. Man kann die
Differenz aber nicht zu 0 machen, da dann der
Differenzenquotient nicht definiert ist.
Dieses Dilemma nennt man Tangentenproblem.
Es gibt ein Werkzeug in der Mathematik, das genau
auf diesen Problemfall anwendbar ist: Die Grenzwertrechnung.
Also: Die Punkte P und Q streben von verschiedenen
Seiten gegen den Punkt S, der Abstand soll gegen 0
gehen, 0 aber nie erreichen.
Seien
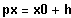und
,
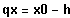wobei h
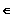R+.
Dann kann man die Grenzwerte
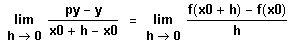und
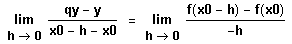aufstellen.
Das entspricht dem rechts- und linksseitigen
Grenzwert an die Stelle x0.
Die Lösung unseres Problems:
Man definiert die Steigung an eine Stelle einer
Kurve als Grenzwert des Differenzenquotienten, den Grenzwert nennt man
dann Differentialquotient.
Stelle x0:
=
{
Existieren rechtsseitiger und linksseitiger
Grenzwert und stimmen sie überein, so existiert der Grenzwert des
Differenzenquotienten, der Differentialquotient. Den Wert des
Differentialquotienten nennt man Ableitungswert der Funktion f(x)
an der Stelle x0 . Schreibweise: f ' (x0) = m .
Die Berechnung des obigen Beispiels:
x --> 2:
LS:
=
=
RS:
=
=
Also gilt
Der Graph von f hat im Punkt ( 2 / 0.5 ) die
Steigung 1
Aufgabe (1): Berechnen Sie die Steigung
der Funktion f an der Stelle x0 = 3
.
Aufgabe (2): Berechnen Sie die Steigung
der Funktion
Geben Sie die Gleichung der Tangente an dieser
Stelle an.
an der Stelle
Lösungen:
Aufgabe (1): Berechnen Sie die Steigung
der Funktion f an der Stelle x0 = 3
.
x --> 3:
LS:
=
RS:
=
Also gilt
Der Graph von f hat im Punkt ( 3 / 2 ) die
Steigung 2
Aufgabe (2): Berechnen Sie die Steigung
der Funktion
Geben Sie die Gleichung der Tangente an dieser
Stelle an.
an der Stelle
x --> -2:
LS:
=
NR:
RS: (analog)
=>
Tangente:
einsetzen:
ist Tangente im Punkt ( -2 / 0 )
