MK 18.3.2004 EigenschaftenFun_Ueb_2.mcd
Übung zur Eigenschaften von Funktionen (2)
(1)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
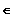R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
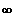2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
3. Berechnen Sie k so, dass der Graph von f Berührpunkte hat.
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
5. Skizzieren Sie den Graphen von f für k = 1.
6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
(2)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
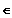R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
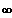2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
3. Berechnen Sie k so, dass der Graph von f Berührpunkte hat.
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
5. Skizzieren Sie den Graphen von f für k = 1.
6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
(3)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
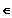R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
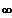2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
3. Berechnen Sie k so, dass der Graph von f keine Berührpunkte hat.
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
5. Skizzieren Sie den Graphen von f für
.
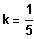6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
Lösung:
(1)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
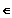R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
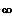2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
Finde
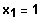
Finde
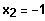
3. Berechnen Sie k so, dass der Graph von f Berührpunkte hat.
Linearfaktorzerlegung
Es existiert ein BP bei -1, falls
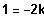, also
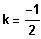
Es existiert ein BP bei 1, falls
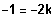, also
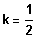
Es existiert ein BP bei 3, falls
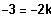, also
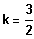
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
Aus den Nullstellen: Symmetrie ist nur möglich, falls der Parameter eine Nullstelle bei -3 produziert.
=>
=>
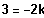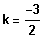
=> Achsensymmetrie
5. Skizzieren Sie den Graphen von f für k = 1.
6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
Der Graph von f(1,x) ist smost für (ca.)
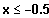und für
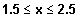und
smofa für (ca.)
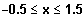und für
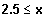
(2)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
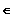R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
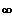2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
Finde
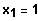
Finde
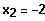
3. Berechnen Sie k so, dass der Graph von f Berührpunkte hat.
Linearfaktorzerlegung
Es existiert ein BP bei -2, falls
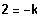, also
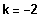oder falls
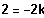, also
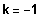
Es existiert ein BP bei 1, falls
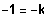, also
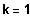oder falls
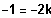, also
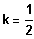
Es existiert ein BP bei 0, falls
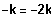, also
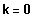
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
Aus den Nullstellen: Symmetrie ist nur möglich, falls der Parameter eine Nullstelle bei -2 und bei 1 produziert.
Das ist nicht möglich, also kann die Funktion nicht symmetrisch werden.
5. Skizzieren Sie den Graphen von f für k = 1.
6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
Der Graph von f(1,x) ist smost für (ca.)
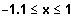und für
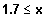und
smofa für (ca.)
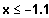und für
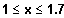
(3)
Gegeben ist die folgende, vom Parameter k abhängige Funktionenschar f.
mit k
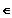R
1. Bestimmen Sie das Grenzverhalten |x|-->
.
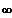2. Ermitteln Sie die Nullstellen in Abhängigkeit von k
Finde
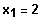
Finde
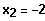
3. Berechnen Sie k so, dass der Graph von f keine Berührpunkte hat.
Linearfaktorzerlegung
Es existiert kein BP bei 5k, falls
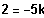, also
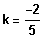(Dann dreifach-SP bei -2)
Es existiert kein BP bei 5k, falls
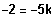, also
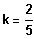(Dann dreifach-SP bei 2)
4. Prüfen Sie, ob es Werte von k gibt, für die der Graph von f symmetrisch ist.
Aus den Nullstellen: Symmetrie ist nur möglich, falls der Parameter einen BP bei 0 produziert.
=>
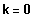
=> Achsensymmetrie
5. Skizzieren Sie den Graphen von f für
.
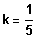6. Lesen Sie die Monotonieintervalle aus dem Graphen ab.
Der Graph von f(1,x) ist smost für (ca.)
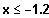und für
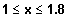und
smofa für (ca.)
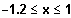und für
