MK 3.6.2003 Symmetrie.mcd
Symmetrie
Wir unterscheiden zwei Arten der Symmetrie: 1.
Punktsymmetrie zum Ursprung und 2. Achsensymmetrie zur Ordinate
(y-Achse).
Punktsymmetrie zum Ursprung
Graphische Symmetrieerzeugung
(1) Probiere eine symmetrische Funktion aus:
Was macht Punkt B, wenn man Punkt A zieht?
(Beschreiben Sie das gegenseitige Verhalten in
Stichpunkten)
(2) Wie wird ein Symmetriepunkt konstruiert?
(Geben Sie die Konstruktionanleitung für
Lineal und Zirkel
in eigenen Worten wieder)
(3) Erzeuge eine eigene Kurve!
(Bestätigen Sie die obigen Punkte spielerisch)
Mathematische Überprüfung
Für eine Punktspiegelung am Ursprung gilt:
Wechselt das Vorzeichen des x-Wertes, dann muss
auch das Vorzeichen des y-Wertes wechseln.
Setzen Sie für das x ein -x in die
Funktionsgleichung ein.
Dann müssen alle Vorzeichen wechseln, es
kommt die negative Funktionsgleichung dabei heraus.
Bsp.:
Sei
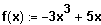
Dann gilt
Das ist genau
f ist punktsymmetrisch zum Ursprung!
Welcher Graph ist
punktsymmetrisch?
=
=> f1 ist punktsymmetrisch
=> f2 ist nicht punktsymmetrisch
=
=> f3 ist punktsymmetrisch
Achsensymmetrie zur y-Achse
Graphische Symmetrieerzeugung
(1) Wie wird ein Symmetriepunkt konstruiert?
(Geben Sie die Konstruktionanleitung für
Lineal und Zirkel
in eigenen Worten wieder)
(2) Erzeuge eine eigene Kurve!
(Bestätigen Sie die obigen Punkte spielerisch)
Mathematische Überprüfung
Für eine Achsenspiegelung an der Ordinate
gilt:
Wechselt das Vorzeichen des x-Wertes, dann darf
das Vorzeichen des y-Wertes nicht wechseln.
Setzen Sie wie bei der Punktsymmetrie für das
x ein -x in die Funktionsgleichung ein.
Dann darf kein Vorzeichen wechseln, es kommt die
alte Funktionsgleichung dabei heraus.
Bsp.:
Sei
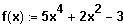
Dann gilt
Das ist genau
f ist achsensymmetrisch zur y-Achse!
Welcher Graph ist
achsensymmetrisch?
=
=> f1 ist achsensymmetrisch
=> f2 ist nicht achsensymmetrisch
=
=> f3 ist achsensymmetrisch
Insgesamt: Setzen Sie -x für alle x in der
Funktionsgleichung ein.
Bleibt nach Vereinfachung alles bei der alten
Funktionsgleichung, so ist die Funktion achsensymmetrisch.
Ändern sich alle Vorzeichen, erhalten Sie
also -f(x), so ist die Funktion punktsymmetrisch.
Erhalten Sie weder f(x) noch -f(x), ist die
Funktion überhaupt nicht symmetrisch.
Aufgaben:
Prüfen Sie rechnerisch auf Symmetrie!
Lösungen:
weder noch, nicht symmetrisch
= f5(x), d.h. achsensymmetrisch
= f6(x), d.h. achsensymmetrisch
= - f7(x), d.h. punktsymmetrisch
= - f8(x), d.h. punktsymmetrisch
weder noch, nicht symmetrisch