MK 3.6.2003 Symmetrie_Ueb.mcd
Übungen zur Symmetrie
Aufgaben:
(1) Welche Funktionen sind symmetrisch?
(2) Wie muss eine ganz rationale Funktion beschaffen sein, damit sie symmetrisch ist?
(3) Gegeben ist die Funktion
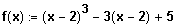. Weisen Sie durch Verschieben (Koordinatentransformation) nach, dass f punktsymmetrisch zu ( 2 / 5 ) ist.
(4) Zu welchem Punkt ist
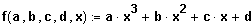punktsymmetrisch?
(5) Gegeben ist die Funktion
. Zu welcher Geraden ist die Funktion symmetrisch?
Lösungen:
(1) Welche Funktionen sind symmetrisch?
und
nicht symmetrisch
AS
und
nicht symmetrisch
PS
PS
AS
AS
und
nicht symmetrisch
PS
(2) Wie muss eine ganzrationale Funktion beschaffen sein, damit sie symmetrisch ist?
Nur ungerade Potenzen von x: Die Funktion ist punktsymmetrisch.
Nur gerade Potenzen von x: Die Funktion ist achsensymmetrisch.
(3) Gegeben ist die Funktion
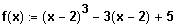. Weisen Sie durch Verschieben (Koordinatentransformation) nach, dass f punktsymmetrisch zu ( 2 / 5 ) ist.
verschiebe f um -2 in x- und -5 in y-Richtung:
fneu ist punktsymmetrisch zu ( 0 / 0 )
f ist punktsymmetrisch zu ( 2 / 5 )
(4) Zu welchem Punkt ist
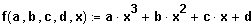punktsymmetrisch?
Verschiebe f um -p in x- und -q in y-Richtung:
Nun müssen die geraden Potenzen verschwinden:
und
und
Bsp.:
(5) Gegeben ist die Funktion
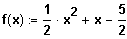. Zu welcher Geraden ist die Funktion symmetrisch?
Parabel in Scheitelform:
f muss zu x = -1 achsensymmtrisch sein.
Nachweis:
Verschiebe f um +1 in x-Richtung:
Achsensymmetrie?
fneu ist achsensymmetrisch zu x = 0.
Also ist f achsensymmetrisch zu x = -1.
