MK 2.4.2009 Vielfachheiten_Ueb1.mcd
Vielfachheiten von Linearfaktoren (Nullstellen)
(1) Gegeben ist die Funktion f1 mit der Funktionsgleichung
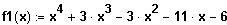
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
(2) Gegeben ist die Funktion f2 mit der Funktionsgleichung
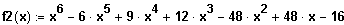
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
(3) Gegeben ist die Funktion f3 mit der Funktionsgleichung
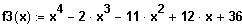
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
(1) Gegeben ist die Funktion f1 mit der Funktionsgleichung
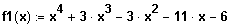
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
Errate
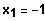
Polinomdivision
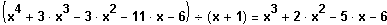
Errate
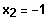
Polinomdivision
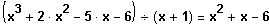
Quadratische Gleichung
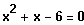
alles klar, noch zwei Lösungen
analog
Linearfaktorzerlegung
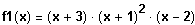
Schnittpunkte bei -3 und 2, Berührpunkt bei -1
Skizze
(2) Gegeben ist die Funktion f2 mit der Funktionsgleichung
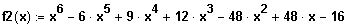
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
Errate

Polinomdivision
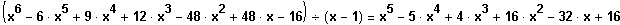
Errate
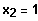
Polinomdivision
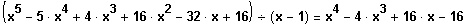
Errate
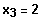
Polinomdivision
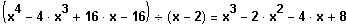
Errate
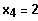
Polinomdivision
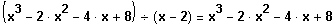
Quadratische Gleichung
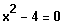
Da braucht man nicht einmal eine Formel !
Linearfaktorzerlegung
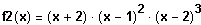
Schnittpunkte bei -2 und 2, Berührpunkt bei 1
Skizze
Details:
(3) Gegeben ist die Funktion f3 mit der Funktionsgleichung
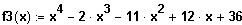
Bestimmen Sie die Nullstellen der Funktion und geben Sie die die Linearfaktorzerlegung an.
Skizzieren Sie den Graphen der Funktion.
Errate
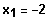
Polinomdivision
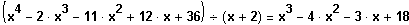
Errate
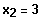
Polinomdivision
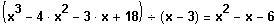
Quadratische Gleichung
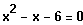
alles klar, noch zwei Lösungen
analog
Linearfaktorzerlegung
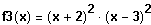
Berührpunkt bei -2 und 3, keine Schnittpunkte
Skizze