MK 3.6.2003 Logarithmusfunktionen.mcd
Logarithmusfunktionen
Lösen sie die folgenden Gleichungen durch
verschärftes Nachdenken. (Lösungen siehe unten)
Definition
x
---> loga(x) mit
a
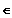 R+\
{1} und x
R+\
{1} und x
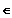 R+
heißt Logarithmusfunktion. (a ist die Basis, x
der Numerus)
R+
heißt Logarithmusfunktion. (a ist die Basis, x
der Numerus)
Wenn
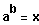 dann ist
dann ist
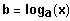 der Logarithmus von x zur Basis a.
der Logarithmus von x zur Basis a.
Oder in Form einer Frage: Mit was muss ich a
potenzieren, um x zu erhalten?
Schreibweise in Mathcad:
Besondere Logarithmusfunktionen
Binärer oder dualer
Logarithmus:
Dekadischer
Logarithmus:
Und der wichtigste: Der natürliche
Logarithmus (Logarithmus naturalis):
Berechne mit dem Taschenrechner:
Methode
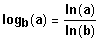
Eigenschaften der Logarithmusfunktionen
Aufgaben:
Probieren Sie mit GEONExT mehrere Basen a
und beantworten Sie dabei die folgenden Fragen.
(1) Haben alle Logarithmusfunktionen gemeinsame
Punkte?
(2) Welche Nullstellen haben die
Logarithmusfunktionen?
(3) Welches Grenzverhalten haben die
Logarithmusfunktionen in Abhängigkeit von a
?
(4) Lesen Sie jeweils die Monotonie ab. Gibt es
Unterschiede?
(5) Sind die Logarithmusfunktionen symmetrisch?
Lösen sie die folgenden Gleichungen durch
verschärftes Nachdenken.
Eigenschaften der Logarithmusfunktionen
(1) Alle Logarithmusfunktionen haben ( 1 / 0 )
gemeinsam.
(2) Das ist die Nullstelle.
(3) Grenzverhalten:
--->
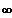
----------------->
--->

----------------->
(4) Monotonie:
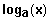 ist streng monoton abnehmend für
ist streng monoton abnehmend für
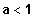
streng monoton zunehmend für
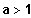
(5) Symmetrie: Keine, aber
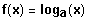 ist an der Abszisse gespiegelt zu
ist an der Abszisse gespiegelt zu
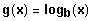 mit
mit