MK 3.6.2003 GebratFun.mcd
Gebrochen-rationale Funktionen
Def.:
Seien
und
zwei ganzrationale Funktionen.
Dann ist
eine gebrochen-rationale Funktion.
Ist
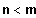so
heißt f echt gebrochen-rational, sonst unecht
gebrochen-rational.
"
"
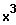Bsp.:
Das ist eine unecht gebrochen-rationale Funktion.
"
"
"
"
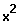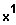Das ist eine echt gebrochen-rationale Funktion.
"
"
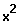Man kann eine unecht gebrochen-rationale Funktion mit
Hilfe der Polynomdivision zerlegen in eine Funktion mit einem
ganzrationalen Anteil r(x) und einem echt gebrochen-rationalen Anteil
s(x).
Bsp.:
:
=
Rest
"Polynomdivision mit REST"
also
und
"Asymptotenform"
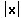weit von der
Definitionslücke entfernt:
f(x)
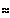
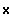nahe bei der
Definitionslücke:
f(x)
Def.:
Nähert sich eine Funktion immer mehr einer
anderen Funktion, so spricht man von einer Asymptotenfunktion.
Bsp.:
Für x
---->
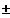
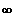nähert
sich r(x) immer mehr f(x).
Also ist r(x) eine Asymptotenfunktion für f(x).
Man kann also für das Grenzverhalten von f(x)
ersatzweise das Grenzverhalten von r(x) untersuchen:
Grenzverhalten:
x ---->
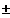
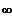
x ---->
------------------->
------------------->
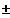
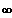
Was geschieht bei der Häufung von
Zähler-/Nennernullstellen?
Probieren Sie es mit dem Beispielprogramm aus.
Definitionsmenge:
D = R \ { Nullstellen des Nennerpolynoms q(x) }
Für f(x): D = R \ { 2 }
Polstellen:
Wenn an einer Stelle x0 der Funktionswert
über alle Grenzen wächst, ist dort eine Polstelle.
x ---->
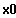
Def.:
Falls
--------------->
so hat f an der Stelle x0
einen Pol.
Bsp.:
f(x) hat an der Stelle x0 = 2
eine Polstelle mit Vorzeichenwechsel.
Also hat f(x) auch eine vertikale Asymptote
(Gleichung x
= 2, keine Funktion!) an
dieser Stelle.
Bsp.:
l(x) hat an der Stelle x0 = 1
eine Polstelle ohne Vorzeichenwechsel.
Also hat l(x) auch eine vertikale Asymptote
(Gleichung x
= 1, keine Funktion!) an
dieser Stelle.
Nullstellen:
Interessante Punkte sind die Nullstellen des
Zählerpolynoms.
Bsp.:
l(x) hat an der Stelle x = - 0.25 eine Nullstelle mit
Vorzeichenwechsel.
(Schnittpunkt)
Bsp.:
m(x) hat an der Stelle x = - 1
eine (doppelte) Nullstelle
ohne Vorzeichenwechsel.
(Berührpunkt)
Hebbare Definitionslücken:
Bsp.:
Man erwartet an der Stelle x0 = 1
entweder einen Pol oder eine Nullstelle.
Man findet jedoch nur eine Lücke bei
ansonsten glattem Kurvenverlauf.
Der Linearfaktor in Zähler und Nenner hebt
sich auf, man kann kürzen.
n(x) hat an der Stelle x = 1
eine hebbare Definitionslücke.
Beispiele:
(1)
Linearfaktor-
zerlegung
gekürzt
Poldiv,
Asymptotenform
D = R \ { -3 ; 4 }
(unecht gebrochen-rationale Funktion)
Hebbare Defintionslücke bei 4
Nullstelle (SP) bei
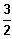
Pol mit VZW bei -3
Grenzverhalten: horizontale Asy y = 2
(2)
Linearfaktor-
zerlegung
Poldiv,
Asymptotenform
(unecht gebrochen-rationale Funktion)
D = R \ { 0 }
kein Hebbare Defintionslücke
Nullstelle (SP) bei
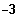
und (BP) bei
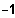
Pol ohne VZW bei 0
Grenzverhalten: schiefe Asy
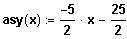
(3)
Linearfaktor-
zerlegung
Poldiv, Asymptotenform
(unecht gebrochen-rationale Funktion)
D = R \ { -2 ; 2 }
keine hebbare Defintionslücke
Nullstelle (vierfach = BP) bei
Pol mit VZW bei -2 und 2
Grenzverhalten:
Asymptotenfunktion
r(x)
Die Funktion ist
achsensymmetrisch.
Linearfaktor-
zerlegung
(4)
(echt gebrochen-rationale Funktion)
D = R \ { -3
; -2 ; 0 ; 2 }
Hebbare Defintionslücke
bei 0
Nullstelle (BP) bei
Nullstelle (SP) bei 3
Pol mit VZW bei -3
Pol mit VZW bei -2
Pol mit VZW bei 2
Grenzverhalten:
Horizontale Asy y=0
