MK 3.6.2003 GebratFun_Ueberblick.mcd
Gebrochen-rationale Funktionen - Überblick
zwei ganzrationale Funktionen.
eine gebrochen-rationale Funktion.
Ist 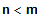 so heißt f echt gebrochen-rational, sonst unecht gebrochen-rational.
so heißt f echt gebrochen-rational, sonst unecht gebrochen-rational.
ist eine unecht gebrochen-rationale Funktion.
ist eine echt gebrochen-rationale Funktion.
Jede unecht gebrochen-rationale Funktion kann mit Hilfe der Polynomdivision zerlegt werden in eine Funktion mit einem ganzrationlen Anteil r(x) und einem echt gebrochen-rationalen Anteil s(x).
D = R \ { Nullstellen des Nennerpolynoms q(x) }
Nullstellen, Pole, hebbare Definitionslücken:
Wir betrachten die Stelle x0:
An der Stelle x0 sei eine a-fache Nullstelle des Zählerpolynoms p(x) und gleichzeitig eine b-fache Nullstelle des Nennerpolynoms q(x).
(Eine reine Zählernullstelle)
Bei x0 gibt es einen Schnittpunkt (SP mit VZW).
Bei x0 gibt es einen Berührpunkt (SP ohne VZW).
Bei x0 gibt es eine hebbare Definitionslücke auf der x-Achse ("Pseudonullstelle").
(1.2.1) Fall: a-b ungerade
Bei x0 sieht die hebbare Definitionslücke aus wie ein Schnittpunkt.
Bei x0 sieht die hebbare Definitionslücke aus wie ein Berührpunkt.
Bei x0 gibt es eine hebbare Definitionslücke (nicht auf der x-Achse).
Bei x0 gibt es eine Polstelle (Unendlichkeitsstelle) der Ordnung b-a
Bei x0 gibt es eine Polstelle mit Vorzeichenwechsel (alternierender Pol).
Bei x0 gibt es eine Polstelle ohne Vorzeichenwechsel.
x----->
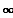
(echt gebrochen-rationale Funktionen)
"Die Abszisse ist horizontale Asymptote"
(unecht gebrochen-rationale Funktionen)
Zerlege f(x) mittels Polynomdivision in die Asymptotenform f(x) = r(x) + s(x)
"Schiefe (schräge) Asymptote"
(mind. quadratischer Term)
(unecht gebrochen-rationale Funktion)
Hebbare Defintionslücke bei 4
Nullstelle (SP) bei 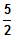
Grenzverhalten: horizontale Asy y = 2
(unecht gebrochen-rationale Funktion)
keine hebbare Defintionslücke
Nullstelle (SP) bei 
Grenzverhalten: schiefe Asy
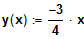
(unecht gebrochen-rationale Funktion)
keine hebbare Defintionslücke
Nullstelle (dreifach = SP) bei 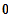
Grenzverhalten:
Asymptotenfunktion
r(x)
D = R \ { -2 ; -1 ; 1 ; 3 }
(echt gebrochen-rationale Funktion)
Hebbare Defintionslücke bei -1
Nullstelle (SP) bei 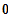
Nullstelle (BP) bei 
Pol mit VZW bei -2
Pol ohne VZW bei 1
Pol mit VZW bei 3
Grenzverhalten:
Horizontale Asy y=0