GS - 05.11.05 - gebro_05_Symmetrie.mcd
Gebrochenrationale Funktionen
- Symmetrische Funktionsgraphen -
1. Achsensymmetrie zur y-Achse
Gegeben ist die Funktion
 .
.
Der Funktionsgraph ist achsensymmetrisch bzgl. der y-Achse, wenn gilt:
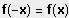
oder: Zähler und Nenner enthalten nur gerade Hochzahlen
oder: Zähler und Nenner enthalten nur ungerade Hochzahlen
Beispiel 1:
ID = IR \ {
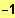 ; 1 }
; 1 }
Vertikale Asymptoten:
Horizontale Asymptote:
Zu zeigen:
Beweis:
Der Graph Gf ist achsensymmetrisch bzgl. der y-Achse.
Beispiel 2:
ID = IR \ { 0 }
Funktionsterm:
Faktorisiert und gekürzt:
Stetig behebbare Def.lücke:
D ( 0 / 9)
Polynomdivision:
in Partialbrüche zerlegt, ergibt
Asymptotische Kurve:
Zu zeigen:
Beweis:
Der Graph Gf ist achsensymmetrisch bzgl. der y-Achse.
2. Punktsymmetrie zum Koordinatenursprung
Gegeben ist die Funktion
 .
.
Der Funktionsgraph ist punktsymmetrisch bzgl. des Koordinatenursprungs, wenn gilt:
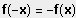
oder: Zähler enthält nur gerade Hochzahlen und Nenner enthält nur ungerade Hochzahlen
oder: Zähler enthält nur ungerade Hochzahlen und Nenner enthält nur gerade Hochzahlen
Beispiel 3:
Funktionsterm:
ID = IR \ {
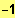 ; 0 ;
; 0 ;
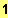 }
}
Faktorisiert und gekürzt:
Stetig behebbare Def.lücke:
D ( 0 / 0)
Horizontale Asymptote:
x-Achse
Zu zeigen:
Beweis:
Der Graph Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
Beispiel 4:
Funktionsterm:
ID = IR \ {
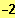 ;
;
 }
}
Polynomdivision mit Rest:
in Partialbrüche zerlegt, ergibt
Schiefe Asymptote:
Zu zeigen:
Beweis:
Der Graph Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
3. Allgemeine Symmetrie (nicht im Lehrplan)
Gegeben ist die Funktion
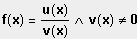 .
.
Der Graph der Funktion f ist entweder punktsymmetrisch bzgl. eines beliebigen Punktes
oder achsensymmetrisch bzgl. einer beliebigen zur y-Achse parallelen Achse.
Der Nachweis der Symmetrie erfolgt über eine Koordinatentransformation vom
Koordinatensystem (X ; Y) in ein neues Koordinatensystem
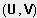 .
.
Speziell bei gebrochenrationalen Funktionen:
Eine unecht-gebrochenrationale Funktion soll nur eine vertikale Asymptote und eine
horizontale bzw. schiefe Asymptote besitzen. Dann gilt:
Der Funktionsgraph ist punktsymmetrisch zum Schnittpunkt der beiden Aymptoten
Beispiel 5:
ID = IR \ {
 }
}
Funktionsterm:
in Partialbrüche zerlegt, ergibt
Polynomdivision mit Rest:
Vertikale Asymptote:
Schiefe Asymptote:
S ( 2 / 1)
Asymptotenschnittpunkt:
Koordinatentransformation:
Transformationsgleichungen in die Funktionsterme eingesetzt:
Asymptote:
Funktionsterme im neuen Koordinatensystem (U ; V)
Nachweis der Punktymmetrie:
Zu zeigen:
Beweis: