MK 3.6.2003
PotenzHyperbelWurzelFun.mcd
Potenzfunktionen, Hyperbelfunktionen,
Wurzelfunktionen
Potenzfunktionen
Def.:
mit n € N
Hyperbelfunktionen
Def.:
mit n € N
Wurzelfunktionen
Def.:
mit n € N\{1}
Aufgabe:
Erstellen Sie mit dem Programm Mathcad für
mindestens 4 Werte von n die Graphen der drei Funktionstypen und
beantworten Sie für jeden Typ die folgenden Fragen (falls
anwendbar).
(1) Defintionsbereich ?
(2) Haben die Graphen gemeinsame Punkte ?
(3) Grenzverhalten ?
(4) Sind die Graphen symmetrisch ?
(5) Monotonie?
Potenzfunktionen
Def.:
mit n € N
(1) Defintionsbereich ?
D = R
(2) Haben die Graphen gemeinsame Punkte ?
(0 / 0) und (1 / 1) alle, (-1 / -1) für n
ungerade, (-1 / 1) für n gerade
(3) Grenzverhalten ?
x --->
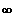
x --->
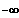
x --->
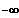
alle
für n ungerade
für n gerade
y -------------------->
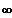
y -------------------->
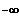
y -------------------->

(4) Sind die Graphen symmetrisch ?
Punktsymmetrie für n ungerade,
Achsensymmetrie für n gerade
(5) Monotonie?
Streng monoton steigend für n ungerade,
streng monoton steigend in R0+
für n gerade,
streng monoton fallend in R0-
für n gerade.
Hyperbelfunktionen
Def.:
mit n € N
(1) Defintionsbereich ?
D = R \ {0}
(2) Haben die Graphen gemeinsame Punkte ?
(1 / 1) alle, (-1 / -1) für n ungerade, (-1 /
1) für n gerade
(3) Grenzverhalten ?
x --->
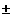
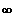
x --->
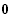
alle
aber:
y -------------------->
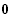
y -------------------->

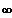
(4) Sind die Graphen symmetrisch ?
Punktsymmetrie für n ungerade,
Achsensymmetrie für n gerade
(5) Monotonie?
Streng monoton fallend in ]
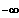 ;0[
;0[
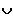 ]0;
]0;
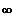 [
für n ungerade,
[
für n ungerade,
streng monoton steigend in ]
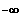 ;0[
für n gerade,
;0[
für n gerade,
streng monoton fallend in ]0;
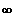 [
für n gerade.
[
für n gerade.
Wurzelfunktionen
Def.:
mit n € N
(1) Defintionsbereich ?
D = R0+
(2) Haben die Graphen gemeinsame Punkte ?
(0 / 0) und (1 / 1) alle
(3) Grenzverhalten ?
x --->

x --->
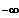
alle
y -------------------->
nicht anwendbar, siehe D
(4) Sind die Graphen symmetrisch ?
nicht anwendbar, siehe D
(5) Monotonie?
Streng monoton steigend für alle