MK 3.6.2003
EigenschaftenPolynomfun.mcd
Eigenschaften ganzrationaler Funktionen
Grenzverhalten
Wie verhält sich der Funktionswert einer
ganzrationalen Funktion für x--->
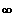oder
x--->
?
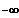Bestimmend ist der Summand mit der höchsten
Potenz von x.
(1) Ungeradzahlige Exponenten ergeben einen
Vorzeichenwechsel im Grenzverhalten, geradzahlige nicht.
(2) Das Vorzeichen des Koeffizienten bestimmt das
Grenzverhalten.
Bsp.:
^---- Bestimmend ist der Summand mit der
höchsten Potenz von x, hier: 3
3 ist ungeradzahlig, also wechselt das Vorzeichen
des Grenzverhaltens.
4 ist positiv.
Also: x ---->
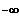x
---->+
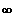
f(x)----------------->
f(x)----------------->+
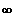
Bsp.:
^---- Bestimmend ist der Summand mit der
höchsten Potenz von x, hier: 7
7 ist ungeradzahlig, also wechselt das Vorzeichen
des Grenzverhaltens.
-5 ist negativ.
Also: x ---->
x
---->+
f(x)----------------->+
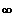f(x)----------------->
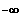
Bsp.:
^---- Bestimmend ist der Summand mit der
höchsten Potenz von x, hier: 4
4 ist geradzahlig, also wechselt das Vorzeichen
des Grenzverhaltens nicht.
-6 ist negativ.
Also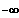: x ---->
x
---->+
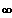
f(x)----------------->
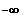f(x)----------------->
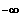
Vielfachheit von Nullstellen
Ein Linearfaktor wird als Differenz (x -
Nullstelle) gebildet.
Die Funktionsgleichung einer ganzrationalen
Funktion kann in Linearfaktoren zerlegt werden.
Dazu muss man die Nullstellen bestimmen.
Ein Beispiel:
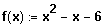hat
die Nullstellen x1= -2 und x2= 3 und somit die
Linearfaktorzerlegung
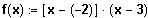
Die Vielfachheit einer Nullstelle ist dann die
Vielfachheit des entsprechenden Linearfaktors.
Das obige Beispiel hat einfache Nullstellen.
Ungeradzahlige Vielfacheiten (1-fache, 3-fache,
5-fache...) ergeben Schnittpunkte,
geradzahlige Vielfacheiten (2-fache, 4-fache,
6-fache...) ergeben Berührpunkte.
Bsp.:
Nullstellen:
Linearfaktorzerlegung:
Es existieren also zwei einfache Nullstellen
(=Schnittpunkte) bei -2 und 3, sowie eine doppelte Nullstelle
(=Berührpunkt) bei -1.
Schnittp.
Berührp.
Schnittp.
Bsp.:
Nullstellen:
Linearfaktorzerlegung:
Es existieren also zwei einfache Nullstellen
(=Schnittpunkte) bei -3 und 3, sowie eine doppelte Nullstelle
(=Berührpunkt) bei 1 und eine dreifache
Nullstelle (=Schnittpunkt) bei -1.
Schnittp.
Schnittp.
Berührp.
Schnittp.
Animation 0 bis 320 , 16 Bilder/s
