MK 3.6.2003
EigenschaftenPolynomfun_2.mcd
Eigenschaften ganzrationaler Funktionen (2)
Monotonie
In welchen Intervallen steigt und fällt der
Graph?
Am
Beispiel:
Anschaulich: Sie sind mit dem Fahrrad immer von
links nach rechts (zunehmende x-Werte) unterwegs. Wenn es bergab geht,
dann fällt
der Graph (streng) monoton. Wenn Sie tüchtig strampeln
müssten, dann steigt
der Graph (streng) monoton.
Mathematische
Definition der Monotonie:
Eine Funktion heißt monoton
zunehmend, wenn
für alle x
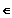D gilt:
Gilt sogar
, dann steigt
der Graph der Funktion streng monoton.
Eine Funktion heißt monoton
abnehmend, wenn
für alle x
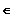D gilt:
Gilt sogar
, dann fällt
der Graph der Funktion streng monoton.
Untersuche
dazu:
unter der Voraussetzung
f ist monoton
zunehmend
f ist monoton
abnehmend
(Anmerkung: Statt streng monoton ist auch echt
monoton gebräuchlich.)
Am
Beispiel:
Annahme:
Graph monoton steigend
Es war
mit
, da Voraussetzung
Man sieht, dass für sehr kleine h
nur Werte
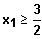in
Frage kommen.
Annahme:
Graph monoton fallend
Rechnung
analog:
Man sieht, dass für sehr kleine h
nur Werte
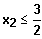in
Frage kommen.
Also: Der Graph von f fällt monoton bis 1.5 und
steigt dann monoton
Ein
anschauliches Beispiel:
Finde die Intervalle, in denen der Graph der Funktion steigt und
fällt.
Beschränktheit
Def.:
Eine Funktion heißt beschränkt, wenn es
eine Zahl K
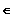R
oder eine Zahl L
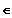R
gibt, so dass gilt:
für alle x
Dann ist K eine obere Schranke.
für alle x
Dann ist L eine untere Schranke.
Die kleinstmögliche obere Schranke
heißt Supremum und die größtmögliche untere
Schranke heißt Infimum.
Bis auf Ausnahmen lässt sich zu diesem
Zeitpunkt eine Schranke nur anschaulich (ohne Beweis) angeben.
Bsp.:
Es gilt
, da
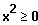
Es gilt auch
Damit wäre -5 eine untere Schranke. Das
Infimum hier wäre 1.
Bsp.:
Es gilt
Hier wäre 2 das Supremum
Bsp.:
Es gilt
Diese Funktion hat eine obere und untere Schranke.
Aufgabe:
Stelle mit Hilfe von GEONExT Schätzungen
für Supremum/Infimum der Graphen fest.
blau
grün
rot
Lösungen: (Die Berechnung mit Mathcad ist in
der 11. Klasse noch nicht nachzuvollziehen)
-->
Ein Infimum existiert nicht, da
-------------->
