MK 4.6.2003 Kurvendisk_Pol_Ueb_5.mcd
Übungen zur Kurvendiskussion (5)
Aufgaben:
Diskutieren Sie die folgenden Funktionen vollständig.
(1)
mit k
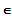R
(1) Grenzverhalten
(2) Nullstellen und ihre Art
(3) Symmetrie
(4) Monotoniebereiche
(5) Extrempunkte und ihre Art
(6) Krümmungsverhalten
(7) Wendepunkte
(8) Wertetabelle, Graph für k = 1
(2)
mit p
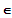R \ { 0 }
(1) Grenzverhalten
(2) Nullstellen und ihre Art
(3) Symmetrie
(4) Monotoniebereiche
(5) Extrempunkte und ihre Art
(6) Krümmungsverhalten
(7) Wendepunkte
(8) Wertetabelle, Graph für k =
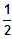
Lösungen:
(1)
mit k
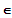R
(1) Grenzverhalten:
(2) Nullstellen:
Linearfaktorzerlegung
-2 für k = 1
1. Fall:
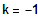=> SP (dreifach) bei 2, SP bei -3
2. Fall:
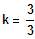=> BP (zweifach) bei 2, BP (zweifach) bei -3
3. Fall: k weder noch => BP (zweifach) bei 2, SP bei -3 und bei -2k
(3) Symmetrie:
Wegen der Nullstellen => Keine Symmetrie
(4) Monotoniebereiche:
1.Ableitung von fk(x)
(Da mind. dopplete NS)
<0 => Keine Nullstellen von D(k), d.h. D(k) > 0 unabhängig von k
=> es gibt immer zwei weitere NS
Linearfaktorzerlegung
Da D(k)>0 ist
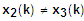
=> Für
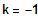gibt es einen BP bei 2 und einen SP, für
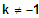gibt es 3 NS mit VZW
1. Fall:
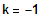
1 NS mit VZW, 1BP
grundsätzlicher Verlauf:
1. NS: Wechsel - dann +
=> fk ist sm abnehmend für
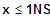
2. NS: kein Wechsel
=> fk ist sm zunehmend für
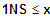
2. Fall:
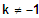
3 NS mit VZW, grundsätzlicher Verlauf:
1. NS: Wechsel - dann +
=> fk ist sm abnehmend für
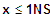
2. NS: Wechsel + dann -
=> fk ist sm zunehmend für
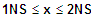
3. NS: Wechsel - dann +
=> fk ist sm abnehmend für
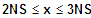
=> fk ist sm zunehmend für
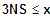
(5) Extrempunkte:
1. Fall:
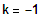1 NS mit VZW, 1BP
Aus der Monotonie:
fallen dann steigen bei 1.NS => Minimum (Terrassenpunkt bei 2)
2. Fall:
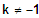3 NS mit VZW
Aus der Monotonie:
fallen dann steigen bei 1.NS => Minimum
steigen dann fallen bei 2.NS => Maximum
fallen dann steigen bei 3.NS => Minimum
(6) Krümmungsverhalten:
<0 => Keine Nullstellen von D(k), d.h. D(k) > 0 unabhängig von k
=> es gibt immer zwei NS
Linearfaktorzerlegung
=> 2 NS mit VZW, grundsätzlicher Verlauf:
1. NS: Wechsel + dann -
=> fk ist konkav (rechts)) für
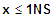
2. NS: Wechsel - dann +
=> fk ist konvex (links) für für
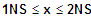
=> fk ist konkav (rechts) für für
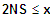
(7) Wendepunkte:
Aus der Krümmung:
Vorzeichenwechsel bei der 1. NS => Wendepunkt
Vorzeichenwechsel bei der 2. NS => Wendepunkt
(8) Wertetabelle, Graph:
(2)
mit p
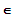R \ { 0 }
(1) Grenzverhalten:
(2) Nullstellen:
=> Zwei doppelte NS (BP) bei + -
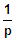
(3) Symmetrie:
= g(p,x) => Die Funktion ist achsensymmetrisch,
unabhängig von p.
(4) Monotoniebereiche:
1.Ableitung von gk(x)
=> es gibt immer drei NS mit VZW
Grundsätzlicher Verlauf:
1. NS: Wechsel - dann +
=> fk ist sm abnehmend für
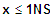
2. NS: Wechsel + dann -
=> fk ist sm zunehmend für
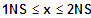
3. NS: Wechsel - dann +
=> fk ist sm abnehmend für
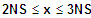
=> fk ist sm zunehmend für
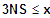
(5) Extrempunkte:
Aus der Monotonie:
fallen auf steigen bei 1.NS => Minimum
(ist
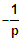falls 0 < p)
steigen auf fallen bei 2.NS => Maximum
fallen auf steigen bei 3.NS => Minimum
(6) Krümmungsverhalten:
=> 2 NS mit VZW, grundsätzlicher Verlauf:
1. NS: Wechsel + dann -
=> fk ist konkav (rechts)) für
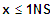
2. NS: Wechsel - dann +
=> fk ist konvex (links) für für
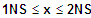
=> fk ist konkav (rechts) für für
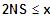
(7) Wendepunkte:
Aus der Krümmung:
Vorzeichenwechsel bei der 1. NS => Wendepunkt
Vorzeichenwechsel bei der 2. NS => Wendepunkt
(8) Wertetabelle, Graph:
