MK 28.1.2004 PolGleichUngl_Ueb.mcd
Übungen zu Polynomfunktionen, Gleichungen,
Ungleichungen
(1)
Gegeben ist die vom reellen Parameter c abhängige Funktion f1.
Bestimmen Sie die Nullstellen von f1. Für welche Werte von c hat
die Funktion Berührpunkte?
(2)
Schneide jeweils die beiden durch die folgenden Funktionsgleichungen
gegebenen Parabeln und Geraden.
(2a)
(2b)
(2c)
(2d)
(2e)
(3)
Gegeben ist die vom reellen Parameter c abhängige Funktion f2 und
die Funktion f3. Bestimmen Sie die Schnittpunkte der beiden Funktionen.
Für welche Werte von c berühren sie sich?
(4)
Gegeben ist die vom reellen Parameter c abhängige Funktion
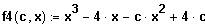 .
.
Bestimmen Sie in Abhängigkeit von c die
Lösungsmenge der Ungleichung
Lösungen:
(1)
Gegeben ist die vom reellen Parameter c abhängige Funktion f1.
Bestimmen Sie die Nullstellen von f1. Für welche Werte von c hat
die Funktion Berührpunkte?
Finde
=> Nullstellen bei -2 , 3 und c
Es gibt Berührpunkte, falls
oder
(2)
Schneide jeweils die beiden durch die folgenden Funktionsgleichungen
gegebenen Parabeln und Geraden.
(2a)
(2b)
(2c)
(2d)
(2e)
(3)
Gegeben ist die vom reellen Parameter c abhängige Funktion f2 und
die Funktion f3. Bestimmen Sie die Schnittpunkte der beiden Funktionen.
Für welche Werte von c berühren sie sich?
Finde
=> Schnittstellen bei -1 , 3/2 und c
Es gibt Berührpunkte, falls
oder
(4)
Gegeben ist die vom reellen Parameter c abhängige Funktion
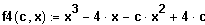 .
.
Bestimmen Sie in Abhängigkeit von c die
Lösungsmenge der Ungleichung
Finde
=> Schnittstellen bei -2 , 2 und c
Es gibt Berührpunkte, falls
oder
Skizzen der einzelnen Fälle:
Fall 1 : c < -2 => L = [ c ; -2 ]
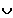 [ 2 ;
¥ [
[ 2 ;
¥ [
Fall 2 : c = -2 => L = { -2 }
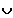 [ 2 ;
¥ [
[ 2 ;
¥ [
Fall 3 : -2 < c < 2 => L = [ -2 ; c ]
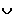 [ 2 ;
¥ [
[ 2 ;
¥ [
Fall 4 : c = 2 => L = [ -2 ; ¥ [
Fall 5 : 2 < c => L = [ -2 ; 2 ]
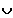 [ c ;
¥ [
[ c ;
¥ [