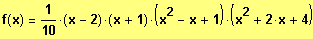GS - 23.10.05 - gara_04_BerechnenNS.mcd
Ganzrationale Funktionen (Polynomfunktionen)
- Berechnung von Nullstellen, Gleichungen höheren Grades -
1. Gleichungen höheren Grades
Gegeben ist der Funktionsterm
.
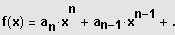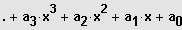
Nullstellenbedingung:
.
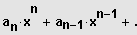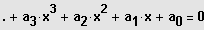
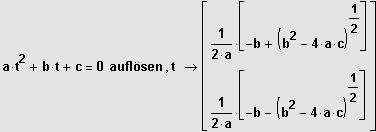
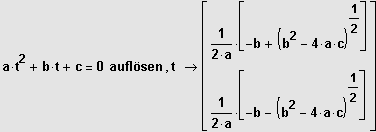
Allgemeine Lösung:
Durch Abspaltung von möglichst vielen Linearfaktoren wird der Grad der Gleichung bis
zum Exponenten
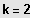erniedrigt, dann Anwendung der Mitternachtsformel.
. . . .
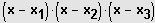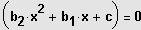
2. Polynomdivision ohne Rest
Ergebnis: Die Polynomdivision ohne Rest erniedrigt den Grad des höchsten Exponenten von x.
Reduktionssatz:
Gegeben ist die Polynomfunktion n-ten Grades
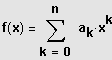mit
.
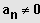Ist
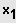eine Lösung der Gleichung
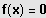, so ist
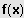durch
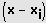teilbar.
Es gilt dann:
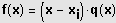, wobei
ein Polynom
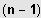-ten Grades ist.
Hinweis:
Die Lösung
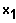wird durch Erraten gefunden, wobei zu zeigen ist, dass gilt:
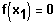
Um dieses Raten so effektiv und kurz wie möglich zu gestalten, folgender
Satz:
Hat die Funktion
.
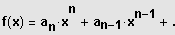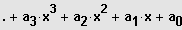
die
ganzzahlige Nullstelle
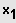, so ist
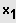ein Teiler von
.
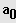Beispiel 1: Gesucht sind die Nullstellen und der vollständig faktorisierte Term
Polynomfunktion:
Nullstellenbedingung:
1. Lösung wird geraten, und zwar probiert man nur die Teiler von 120:
keine Lösung
Lösung
Polynomdivision:
in Partialbrüche zerlegt, ergibt
Lösung der quadratischen Gleichung:
Mathcad - Lösung:
Drei einfache Nullstellen
Faktorisierter Funktionsterm:
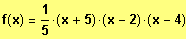
Beispiel 2: Gesucht sind die Nullstellen und der vollständig faktorisierte Term
Polynomfunktion:
Nullstellenbedingung:
1. Lösung wird geraten, und zwar probiert man nur die Teiler von 40.
keine Lösung
keine Lösung
Lösung
Polynomdivision:
ergibt
Lösung der kubischen Gleichung:
Definition der Polynomfunktion:
2. Lösung wird geraten, und zwar probiert man nur die Teiler von 10.
keine Lösung
Lösung
Polynomdivision:
in Partialbrüche zerlegt, ergibt
Lösung der rein quadratischen Gleichung:
Mathcad - Lösung:
Vier einfache Nullstellen
Faktorisierter Funktionsterm:
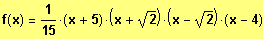
3. Substitution
Bei achsensymmetrischen Funktionen 4. Grades treten nur gerade Potenzen von x auf:
.
Die Nullstellenbedingung
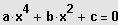liefert eine biquadratische Gleichung, die
mit
der Substitution
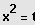über die Lösungsformel für quadratische Gleichungen und
anschließender Resubstitution gelöst wird.
Es gilt:
Beispiel 3: Gesucht sind die Nullstellen und der vollständig faktorisierte Term
Polynomfunktion:
Nullstellenbedingung:
Substitution:
Lösung der quadratischen Gleichung:
Resubstitution:
Vier einfache
Nullstellen
Mathcad - Lösung:
Faktorisierter Funktionsterm:
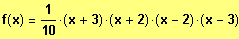
Beispiel 4: Gesucht sind die Nullstellen und der vollständig faktorisierte Term
Polynomfunktion:
Nullstellenbedingung:
Substitution:
Lösung der quadratischen Gleichung:
keine
Lösung
Resubstitution:
Mathcad - Lösung:
Lösung
Lösung
Zwei einfache
Nullstellen
keine Lösung
keine Lösung
Faktorisierter Funktionsterm:
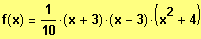
Beispiel 4: Gesucht sind die Nullstellen und der vollständig faktorisierte Term.
Polynomfunktion:
Nullstellenbedingung:
Substitution:
Lösung der quadratischen Gleichung:
identische
Lösungen
Resubstitution:
Mathcad - Lösung:
Lösung
Lösung
Zwei zweifache
Nullstellen
Lösung
Lösung
Faktorisierter Funktionsterm:
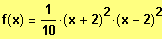
4. Erweiterung der Substitution
Bei Funktionen höheren Grades der "Bauart biquadratisch" treten nur die Potenzen
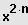bzw.
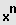auf:
.
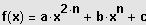Die Nullstellenbedingung
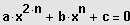liefert auch hier eine biquadratische
Gleichung,
die mit der Substitution
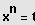über die Lösungsformel für quadratische
Gleichungen und anschließender Resubstitution gelöst wird.
Es gilt:
Beispiel 5: Gesucht sind die Nullstellen und der vollständig faktorisierte Term
Polynomfunktion:
Nullstellenbedingung:
Substitution:
Lösung der quadratischen Gleichung:
Lösung
Resubstitution:
keineLösung
keineLösung
Lösung
keineLösung
keineLösung
Mathcad -Lösung:
Lösung
Zwei zweifache
Nullstellen
Lösung
keine Lösung
keine Lösung
keine Lösung
keine Lösung
Das Faktorisieren ist hier nicht so ganz einfach, weil es nur zwei Linearfaktoren gibt.
1. Möglichkeit: Zweimalige Polynomdivision
Funktionsterm:
Raten:
ist Lösung
1. Polynomdivision:
ergibt
Raten:
ist Lösung
2. Polynomdivision:
ergibt
keine weitere Zerlegung
Faktorisierter Funktionsterm:
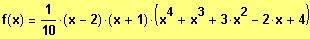
2. Möglichkeit: Teilweises Faktorisieren und dann Anwendung einer Zerlegungsformel
Faktoren vor der Resubstitution:
Zerlegungsformeln:
Mathcad - Lösung:
Faktorisierter Funktionsterm:
