MK 3.6.2003 Quadfunktion.mcd
Der Graph quadratischer Funktionen
Def.:
Funktionen der Form
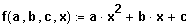heißen quadratische Funktionen. Mit b,c € R, a € R\{0}.
Bsp.:
Seien
Dann bleibt
Zeichne den Graphen der Funktion fn
Wertetabelle:
Graph:
Es handelt sich um eine
Normalparabel.
Aufgabe:
Erkunde den Einfluss des Parameters c.
Aufgabe:
Erkunde den Einfluss des Parameters b.
Wie könnte man einen Parameter festlegen, der
ein Verhalten ähnlich wie c in y-Richtung aber für die
x-Richtung ermöglicht?
Aufgabe:
Erkunde den Einfluss eines Parameters p.
Aufgabe:
Erkunde den Einfluss des Parameters a.
Alles zusammen: Wie sieht der Graph von
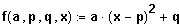aus?
Lösungen:
Der Parameter c bewirkt eine Verschiebung der
Normalparabel
um c in y-Richtung.
Man erkennt keine eindeutige Zuordnung.
Der Parameter p bewirkt eine Verschiebung der
Normalparabel
um +p in x-Richtung. (Vorzeichen!)
Der Parameter a bestimmt Form und Öffnung.
Ist a<0, so ist die Parabel nach unten
geöffnet.
Ist a>0, so ist die Parabel nach oben
geöffnet.
Ist |a|<1, so ist die Parabel gestaucht im
Vergleich zur Normalparabel. (Badewannenartiger!)
Ist |a|>1, so ist die Parabel gestreckt im
Vergleich zur Normalparabel. (Lang und schlank!)
Alles zusammen:
Der Parameter a bestimmt Form und Öffnung.
Der Parameter p bewirkt eine Verschiebung in
x-Richtung.
Der Parameter q bewirkt eine Verschiebung in
y-Richtung.
