EL / GS - 23.08.05 - b1_quadGl.mcd
Quadratische Gleichungen
Definition:
Eine Bestimmungsgleichung mit der Definitionsmenge ID
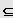G heißt quadratisch (oder
zweiten Grades), wenn sie auf die Form
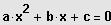mit a, b, c
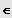IR und
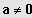
gebracht werden kann.
Bezeichnung: Gleichungen, die die gleiche Lösungsmenge haben, heißen äquivalent.
Regel:
Ist die quadratische Gleichung in der Hauptform gegeben, dann lässt sie sich in folgende
äquivalente Gleichung umformen:
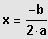
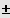
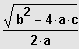
Speziell:
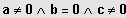: Reinquadratische Gleichung
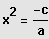, Lösung durch Wurzelziehen.
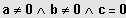: Quadratische Gleichung
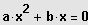, Lösung durch Ausklammern.
Bestimmung der Lösungsmenge:
(1) Sei
;
;
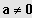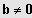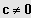und
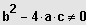
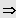
Zwei Lösungen
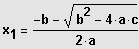und
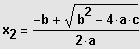IL = {
;
}
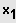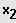(2) Sei
;
;
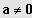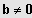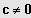und
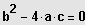
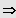Eine Lösung
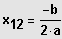IL = {
}
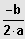(3) Sei
;
;
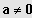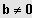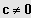und
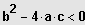
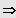Keine Lösung IL = { }
(4) Sei
;
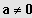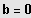; und
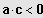
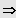Zwei Lösungen
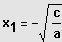und
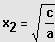IL = {
;
}
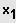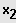(5) Sei
;
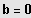; und
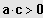
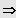Keine Lösung IL = { }
(6) Sei
;
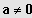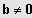; und
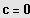
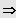Zwei Lösungen
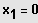und
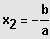IL = {
;
}
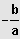Beispiele dazu siehe auf den nächsten Seiten.
Aufgabe 1:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
ID = IR
Lösung:
IL = {2; 4}
Teilaufgabe b)
Parabel:
Lösung = Nullstellen der Parabel:
Die Parabel hat zwei einfache Nullstellen:
NS1(2 / 0)
NS2(4 / 0)
Graphische Lösung der Gleichung:
Aufgabe 2:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
ID = IR
Lösung:
IL = {3}
Teilaufgabe b)
Parabel:
äquivalenter Funktionsterm:
Lösung = Nullstellen der Parabel:
Die Parabel hat eine zweifache Nullstellen:
NS1/2(3 / 0)
Graphische Lösung der Gleichung:
Aufgabe 3:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
ID = IR
Lösung:
In IR keine Lösung!
IL = { }
Teilaufgabe b)
Parabel:
in IR
nicht
definiert
Lösung = Nullstellen der Parabel:
Die Parabel hat keine Nullstellen.
Graphische Lösung der Gleichung:
Aufgabe 4:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
äquivalente Gleichung:
ID = IR
Lösung:
IL = {
;
}
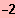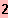Teilaufgabe b)
Parabel:
Lösung = Nullstellen der Parabel:
Die Parabel hat zwei einfache Nullstellen:
NS1(
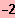/ 0 )
NS2( 2 / 0 )
Graphische Lösung der Gleichung:
Aufgabe 5:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
äquivalente Gleichung:
ID = IR
Lösung:
in IR keine Lösung
IL = { }
Teilaufgabe b)
Parabel:
Lösung = Nullstellen der Parabel:
Die Parabel hat keine Nullstellen:
Graphische Lösung der Gleichung:
Aufgabe 6:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
äquivalente Gleichung:
ID = IR
Lösung:
IL = {
;
}
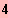Teilaufgabe b)
Parabel:
Lösung = Nullstellen der Parabel:
Die Parabel hat zwei einfache Nullstellen:
Graphische Lösung der Gleichung:
Aufgabe 7:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
ID = IR
linke Seite:
rechte Seite:
in die Hauptform bringen:
IL = {2; 4}
Lösung:
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
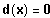
Graphische Lösung der Gleichung:
Aufgabe 8:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Gleichung:
ID = IR
linke Seite:
rechte Seite:
in die Hauptform bringen:
IL = { 0; 6 }
Lösung:
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
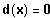
Graphische Lösung der Gleichung:
