GS - 23.08.05 - c1_hoehereGl.mcd

Gleichungen höheren Grades

Definition:
Eine Gleichung der Form 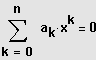mit der Definitionsmenge ID 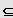IR und
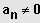
heißt "Gleichung n-ten Grades".

Schreibweise: + . . . +

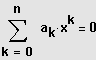
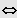
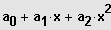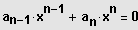
Allgemeine Lösung:
Durch Abspaltung von möglichst vielen Linearfaktoren wird der Grad der Gleichung bis zum
Exponenten 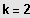erniedrigt, dann Anwendung der Mitternachtsformel.
   . . . .

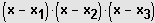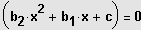
1. Möglichkeit: "Reine" Gleichung höheren Grades

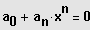
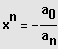
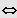
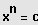
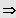Lösung durch Ziehen der n-ten Wurzel.
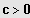
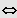
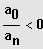
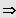
1. Fall: n gerade und 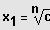und
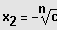
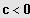
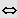
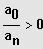
   2. Fall: n gerade und 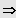Gleichung besitzt keine Lösung in IR
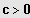
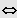
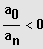
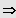
3. Fall: n ungerade und 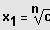(nur eine Lösung!)
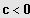
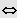
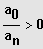
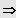
4. Fall: n ungerade und 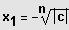(nur eine Lösung!)

2. Möglichkeit: Erzeugung der Linearfaktoren durch Ausklammern

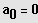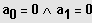oder oder 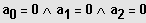usw.
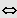Ausklammern der höchstmöglichen Potenz von x und Produkt gleich Null.

z.B. bei einer Gleichung 4. Grades: 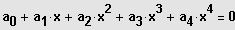speziell:

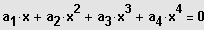
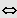
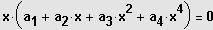
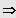
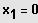
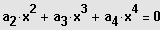
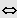
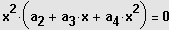
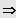
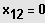
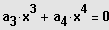
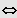
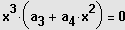
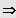
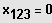
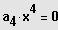
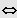
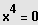
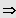
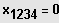
3. Möglichkeit: Gleichung besitzt eine ganzzahlige Lösung

Polynomdivision ohne Rest
z. B. bei einer Gleichung 3. Grades:
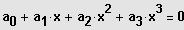
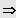
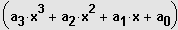ist Lösung ist durch 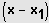teilbar.
Es gilt: :

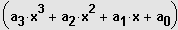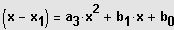
4. Möglichkeit: Biquadratische Gleichungen

1. Fall:
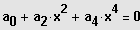
Substitution
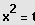
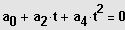
Lösung der quadratischen Gleichung und Resubstituition liefert die
reinquadratischen Gleichungen: 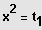     und
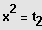
     Auflösen durch Wurzelziehen, sofern 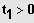bzw. .
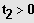              Lösungen:     ; ; ; ;
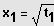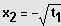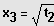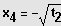1. Fall:
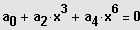
Substitution
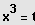
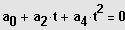
Lösung der quadratischen Gleichung und Resubstituition liefert die
              reinen kubischen Gleichungen: 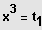    und
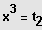
                  Auflösen durch Wurzelziehen.
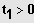
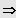
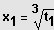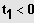
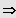
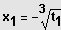
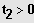
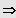
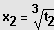Lösungen: bzw.
            bzw.

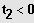
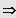
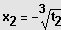
5. Möglichkeit: Gleichung besitzt keine ganzzahlige Lösung und ist nicht biquadratisch

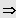numerische Verfahren, z.B.
Tangentenverfahren (Newton'sche Näherung), Sekantenverfahren (Regula Falsi),
        Intervallhalbierung, usw.

Beispiele dazu siehe auf den nächsten Seiten.

Aufgabe 1:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Auflösen nach 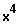und 4. Wurzel ziehen.

IL = { ; }

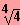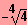Lösung:

Lösung

Lösung

keine Lösung in IR

keine Lösung in IR

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

Linke Funktion:

Rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

Graphische Lösung der Gleichung:

Aufgabe 2:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösung: Gleichung besitzt keine Lösung in IR.

IL = { }

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

Linke Funktion:

Rechte Funktion:

Differenzfunktion:

besitzt keine Nullstellen

Aufgabe 3:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Auflösen nach 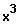und 3. Wurzel ziehen.

IL = { }

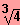Lösung:

Lösung

keine Lösung in IR

keine Lösung in IR

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

Linke Funktion:

Rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

Aufgabe 4:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Auflösen nach 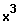und 3. Wurzel ziehen.

Bemerkung:

IL = { }

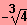Lösung:

Lösung

keine Lösung in IR

keine Lösung in IR

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

Linke Funktion:

Rechte Funktion:

Differenzfunktion:

Aufgabe 5:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Polynomdivision ohne Rest.

Lösung:

Definition der Polynomfunktion:

1. Lösung wird geraten, und zwar probiert man nur die Teiler von 120:

keine Lösung

Lösung

Polynomdivision:

in Partialbrüche zerlegt, ergibt

Lösung der quadratischen Gleichung:

Mathcad - Lösung:

IL = { ; ; }

Teilaufgabe b)

Graphische Lösung der Gleichung:

Aufgabe 6:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Polynomdivision ohne Rest.

Lösung:

Definition der Polynomfunktion:

1. Lösung wird geraten, und zwar probiert man nur die Teiler von 40.

keine Lösung

keine Lösung

Lösung

Polynomdivision:

in Partialbrüche zerlegt, ergibt

Lösung der kubischen Gleichung:

Definition der Polynomfunktion:

2. Lösung wird geraten, und zwar probiert man nur die Teiler von 10.

keine Lösung

Lösung

Polynomdivision:

in Partialbrüche zerlegt, ergibt

Lösung der rein quadratischen Gleichung:

Mathcad - Lösung:

IL = { ; ; ; }

Teilaufgabe b)

Graphische Lösung der Gleichung:

Aufgabe 7:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Substitution

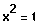
Lösung:

Substitution:

Lösung der quadratischen Gleichung:

Resubstitution:

Mathcad - Lösung:

IL = { ; ; ; }

Teilaufgabe b)

Definition der Polynomfunktion:

Graphische Lösung der Gleichung:

Aufgabe 8:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Substitution

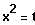
Lösung:

Substitution:

Lösung der quadratischen Gleichung:

keine
Lösung

Resubstitution:

Mathcad - Lösung:

Lösung

Lösung

IL = { ; }

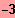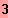keine Lösung

keine Lösung

Teilaufgabe b)

Definition der Polynomfunktion:

Graphische Lösung der Gleichung:

Aufgabe 9:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Substitution

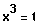
Lösung:

Substitution:

Lösung der quadratischen Gleichung:

Lösung

keine Lösung

Resubstitution 1:

keine Lösung

Lösung

Resubstitution 2:

keine Lösung

keine Lösung

Mathcad - Lösung:

Lösung

IL = { ; }

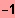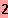Lösung

keine Lösung

keine Lösung

keine Lösung

keine Lösung

Teilaufgabe b)

Definition der Polynomfunktion:

Graphische Lösung der Gleichung:

Aufgabe 10:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR

Lösungsweg: Newton'sches Verfahren (Formelsammlung Seite 20):

Ist 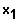ein Näherungswert für die Nullstelle von 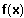, so ist

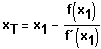
ein neuer, im allgemeinen besserer Näherungswert.

Lösung:

Polynomfunktion:

1. Ableitung:

Funktionswerte:

Lösung im Intervall ] ; [

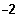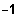Startwert:

1. Näherung:

2. Näherung:

3. Näherung:

4. Näherung:

Mathcad - Lösung:

Lösung

keine Lösung

keine Lösung

Teilaufgabe b)

Definition der Polynomfunktion:

Graphische Lösung der Gleichung:

Impressum · Datenschutz