EL / GS - 23.08.05 - d1_Bruchgl.mcd

Bruchgleichungen

Definition:
Eine Gleichung, bei der eine Variable x auch im Nenner vorkommt, ohne dass man sie
kürzen kann, heißt Bruchgleichung. 

Bezeichnung: Gleichungen, die die gleiche Lösungsmenge haben, heißen äquivalent.

Bestimmung der Lösungsmenge:
Man löst eine Bruchgleichung, indem man die Definitionsmenge bestimmt (Nenner ungleich
Null), die Gleichung mit dem Hauptnenner multipliziert und die so entstehende Gleichung
löst.  

Definition:
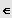Eine Gleichung mit a,b,c,d IR und heißt lineare Bruchgleichung.

Bestimmung der Lösungsmenge:
(1) Man löst die Bruchgleichung 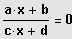, indem man die Definitionsmenge ID = IR \ { 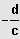} bestimmt, die Gleichung mit dem Hauptnenner 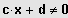multipliziert und die so ent-
stehende Gleichung 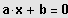       löst.
(2) Man löst die Bruchgleichung 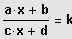(k = Konstante), indem man die Definitions-
menge ID = IR \ { 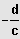      } bestimmt und die Bruchgleichung in die Form bringt.

Die linke Seite wird sodann auf den Hauptnenner gebracht, beide Terme zusammenge-
fasst und die neue Gleichung 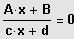        nach Schema (1) gelöst.

Beispiele dazu siehe auf den nächsten Seiten.

Aufgabe 1:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR \ { }

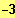Lösung:

IL = { }

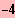Durch Multiplizieren mit dem Nenner Umformung der Bruchgleichung in eine lineare Gleichung:

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

linke Funktion:

rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

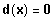
Graphische Lösung der Gleichung:

Aufgabe 2:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR \ { 2 ; 4 }

Lösung:

IL = { 5 }

Durch Multiplizieren mit dem Hauptenner Umformung der Bruchgleichung in eine lineare Gleichung:

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

linke Funktion:

rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

Graphische Lösung der Gleichung:

Aufgabe 3:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR \ { 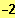; 2 }

Lösung:

IL = { 0 }

Durch Multilpizieren mit dem Hauptnenner Umformung der Bruchgleichung in eine lineare Gleichung:

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

linke Funktion:

rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

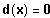
Graphische Lösung der Gleichung:

Aufgabe 4:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR \ { 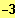; 3 }

Lösung:

IL = ID

Durch Multilpizieren mit dem Hauptnenner Umformung der Bruchgleichung in eine lineare Gleichung:

also eine Identität

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

linke Funktion:

rechte Funktion:

Differenzfunktion:

Bestimme diejenigen x-Werte, für die gilt:

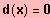
Graphische Lösung der Gleichung:

Aufgabe 5:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen

Teilaufgabe a)

Gleichung:

ID = IR\ { 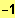; 0 ; 1}

Lösung:

IL = { }

Durch Multilpizieren mit dem Hauptnenner Umformung der Bruchgleichung in eine quadratische
Gleichung:

Teilaufgabe b)

Darstellung der Gleichung mit Funktionen:

linke Funktion:

rechte Funktion:

Differenzfunktion:

Graphische Lösung der Gleichung:

Impressum · Datenschutz