EL / GS - 23.08.05 - e1_trigGl.mcd
Goniometrische Gleichungen
Definition:
Gleichungen, in denen die Variable als Argument von Winkelfunktionen vorkommen,
nennt man "goniometrische Gleichungen".
Lösungsweg:
Mit Hilfe der Formeln der Formelsammlung Seite 38 bis 39 lässt sich in vielen Fällen eine
zur gegebenen Gleichung äquivalente Gleichung finden, deren Lösungsmenge unmittel-
bar angegeben werden kann. Durch die Vielfalt bei goniometrischen Gleichungen können
nur für einfache ausgewählte Typen systematische Verfahren angegeben werden.
Es sind dies z.B.:
(1) Gleichungen mit nur einer Winkelfunktion
(2) Gleichungen mit zwei Winkelfunktionen desselben Arguments
(3) Gleichungen mit zwei Winkelfunktionen verschiedener Argumente
Beispiele dazu siehe auf den nächsten Seiten.
Aufgabe 1:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichungstyp (1):
ID = IR
Lösungsansatz:
Ersetzen des Terms mit doppeltem Arg. mit Hilfe des Additionstheorems:
Umformung von
Einsetzen:
Ausklammern:
Lösungsmenge Fall 1:
Standardwerte in [ 0 ; 2
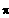 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Lösungsmenge Fall 2:
Standardwerte in [ 0 ; 2
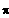 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Ausgabe der Lösungen:
Teilaufgabe b)
Darstellung der goniometrischen Gleichung durch den Graph einer
trigonometrischen Funktion:
Aufgabe 2:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichungstyp (2):
ID = IR
Lösungsansatz:
Reduzieren auf eine Winkelfunktion mit Hilfe des trigonom. Pythagoras:
Ausklammern:
Umformung von
Einsetzen:
Vereinfachen:
Lösungsmenge Fall 1:
Standardwerte in [ 0 ; 2
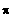 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Lösungsmenge Fall 2:
Standardwerte in [ 0 ; 2
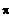 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Ausgabe der Lösungen:
Teilaufgabe b)
Darstellung der goniometrischen Gleichung durch den Graph einer
trigonometrischen Funktion:
Aufgabe 3:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichungstyp (3):
ID = IR
Lösungsansatz:
Ersetzen des Terms mit doppeltem Argum. mit Hilfe des Additionstheorems:
Umformen liefert:
quadratische Gleichung:
Substitution:
Einsetzen:
Lösungsmenge Fall 1:
Standardwerte in [ 0 ; 2
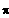 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Lösungsmenge Fall 2:
Standardwerte in [ 0 ; 2
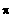 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Ausgabe der Lösungen:
Probe:
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Lösung
Teilaufgabe b)
Darstellung der goniometrischen Gleichung durch den Graph einer
trigonometrischen Funktion:
Aufgabe 4:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichungstyp (1):
ID = IR
Lösungsansatz:
Substitution und Lösen der quadratischen Gleichung.
Substitution:
Lösungsmenge Fall 1:
Standardwerte in [ 0 ; 2
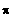 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Lösungsmenge Fall 2:
Standardwerte in [ 0 ; 2
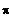 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Ausgabe der Lösungen:
Teilaufgabe b)
Darstellung der goniometrischen Gleichung durch den Graph einer
trigonometrischen Funktion:
Aufgabe 5:
a) Bestimmen Sie von der gegebenen Gleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichungstyp (2):
ID = IR
Lösungsansatz:
Reduzieren auf eine Winkelfunktion mit Hilfe des trigonom. Pythagoras.
Substitution:
Einsetzen:
Quadrieren:
Umformen liefert:
Ausklammern:
Lösungsmenge Fall 1:
Standardwerte in [ 0 ; 2
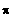 ]
]
Allgemeine Lösung:
k Î Z (k kann beliebig gewählt werden)
Lösungsmenge Fall 2:
Standardwerte in [ 0 ; 2
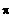 ]
]
k Î Z (k kann beliebig gewählt werden)
Ausgabe der Lösungen:
Probe:
Lösung
Lösung
Lösung
Lösung
keine Lösung
keine Lösung
keine Lösung
keine Lösung
Lösung
Lösung
Lösung
Lösung
Teilaufgabe b)
Darstellung der goniometrischen Gleichung durch den Graph einer
trigonometrischen Funktion: