GS -23.08.05 - g1_logGl.mcd
Logarithmische Gleichungen
Definition:
Eine Gleichung der Form
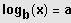mit
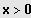, a
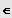IR und b
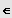IR+ \ {1} heißt
Logarithmusgleichung.
Besondere Basen:
Basis
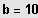heißt Dekadischer Logarithmus:
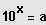
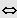
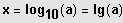
Basis
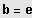heißt Natürlicher Logarithmus:
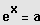
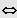
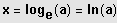Basis
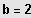heißt Zweier - Logarithmus:
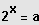
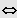
Bestimmung der Lösungen: Zur Anwendung kommen die
- Potenzgesetze: FS Seite 15 / C
- Monotoniegesetze für Potenzen: FS Seite 16 / B
- Rechengesetze für Logarithmen: FS Seite 16 / B
- Indentitäten:
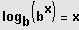und
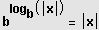mit
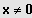
- Basisumrechnung in die "Taschenrechnerbasen" 10 bzw. e: FS Seite 16 / C
Lösung:
(1) Bringe die Logarithmusgleichung durch Erheben in die Potenz zur Basis b in die Form
(2) Bei unterschiedlichen Basen stelle beide Seiten der Logarithmusgleichung als Loga-
rithmus derselben Basis dar und löse dann wieder durch Potenzieren beider Seiten.
Beispiele dazu siehe auf den nächsten Seiten.
Schreibweise in Mathcad:
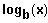entspricht
.
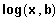Aufgabe 1:
a) Bestimmen Sie die Lösungsmenge folgender Gleichung in der Grundmenge IR.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichung:
ID = ]
;
[
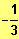Lösungsweg: Potenzieren.
Lösung:
IL = {
}
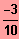Mathcad:
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
Graphische Lösung der Gleichung:
Aufgabe 2:
a) Bestimmen Sie die Lösungsmenge folgender Gleichung in der Grundmenge IR.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichung:
ID = IR \ [
;
]
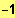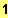Lösungsweg : Substitution des Arguments
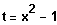, Potenzieren und Basis umrechnen,
Resubstitution und nach x auflösen.
Lösung:
IL = {
}
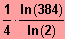Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
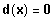
Graphische Lösung der Gleichung:
Aufgabe 3:
a) Bestimmen Sie die Lösungsmenge folgender Gleichung in der Grundmenge IR.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichung:
ID = IR
Lösungsansatz: Substitution des Terms
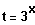, quadratische Gleichung lösen,
Resubstitution und nach x auflösen
keine Lösung
Lösung:
IL = {
}
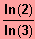Lösung
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
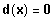
Graphische Lösung der Gleichung:
Aufgabe 4:
a) Bestimmen Sie die Lösungsmenge folgender Gleichung in der Grundmenge IR.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichung:
ID = IR
Lösungsansatz: Substitution des Terms
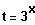, gleichartige Terme zusammenfassen,
quadratische Gleichung lösen, Resubstitution und nach x auflösen
Lösung:
IL = {
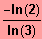; 1 }
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
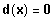
Graphische Lösung der Gleichung:
Aufgabe 5:
a) Bestimmen Sie die Lösungsmenge folgender Gleichung in der Grundmenge IR.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Gleichung:
ID = IR
Lösungsansatz: Aufspalten der Potenzen , x-Potenz und Zahlenpotenz separieren ,
Logarithmieren und Basisumrechnen.
Lösung:
IL = {
}
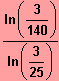Aufspalten:
erweitert auf
Separieren:
Logarithmieren:
Teilaufgabe b)
Darstellung der Gleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
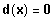
Graphische Lösung der Gleichung: Variante A
Darstellung der Gleichung mit Funktionen: Variante B
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Bestimme diejenigen x-Werte, für die gilt:
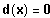
Graphische Lösung der Gleichung: Variante B
