MK 3.6.2003 QuadGleichung.mcd
Die quadratische Gleichung
Allgemein kann man eine quadratische Gleichung
durch quadratische Ergänzung lösen.
Man will eine binomische Formel erzeugen.
< das wäre das 1. Binom >
Alles, was stört, aus der großen
Klammer raus.
Vereinfachen.
Reste auf die andere Seite.
Binom ausnutzen.
Durch a.
Hauptnenner.
Abkürzung: Sei
(Mit D=Diskriminante, Bestimmende)
Also
Auf der linken Seite steht ein Quadrat. Links kann
der Ausdruck also nie negativ werden. Der Ausdruck rechts schon. Dann
hätte die Gleichung keine Lösung.
Man braucht also eine Fallunterscheidung.
(1) Fall: Sei D<0.
Dann wissen wir sofort: L = {}
(2) Fall: Sei D=0.
Dann gilt:
Es gibt genau eine Lösung: L = {
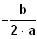 }
}
(3) Fall: Sei D>0
Dann kann man die Wurzel ziehen und man bekommt
endlich zwei Lösungen:
und
und
Bsp.:
D>0, also (3) Fall.
L = { -2 ; 2 }
Bsp.:
D=0, also (2) Fall.
L = { 1 }
Bsp.:
D<0, also (1) Fall.
Ohne jede weitere Rechnung sieht man: L = {}
Die drei Beispiele entsprechen übrigens den
Beispielfunktionen von oben. So kann man den Verlauf des entsprechenden
Graphen in Beziehung zur Anzahl der Nullstellen einer quadratischen
Gleichnung erkennen.
Also genügt es, zur Bestimmung des Falles nur
den Zähler auszuwerten. Man bekommt so eine neue Diskriminante.
Wenn man sich D genauer ansieht, bemerkt man, dass
der Nenner nichts zum Vorzeichen beiträgt (Da immer positiv).
Dann muss man aber auch die Formel für Fall
(3) etwas bearbeiten:
werden zu
Ein letztes Face-Lifting:
analog
Bemerkung:
Wenn man die Gleichung als erstes durch a dividiert
und die Koeffizienten dann umtauft
erhält man die beliebte (weil effiziente)
p-q-Formel (Herleitung analog):
mit
zur Bestimmung der Fälle