MK 3.6.2003 Polynomdivision_GLoes.mcd
Lösen von Gleichungen durch Polynomdivision
Polynomgleichungen vom Grade n>2 lassen sich unter bestimmten Bedingungen durch das Verfahren Polynomdivision lösen.
Verfahren Löse Polynomgleichungen
Am Beispiel: Löse
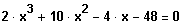
1. Schritt: Versuche eine Lösung zu erhalten: Graph zeichnen, probieren
Eine Lösung könnte 2 sein
2 in die Funktionsgleichung einsetzen:
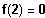Also ist 2 eine Lösung
Umformung:
----->
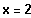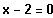
Wenn 2 eine Lösung ist, steckt der Linearfaktor
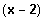im Funktionsterm.
2. Schritt: Der Linearfaktor wird abdividiert, das vereinfacht die Gleichung um einen Grad.
:
=
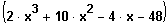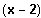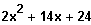Das Beispiel vom letzen Mal.
3. Schritt: Die quadratische Gleichung wird gelöst.
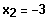und
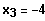
Die Polynomgleichung lässt sich als linearfaktorzerlegt darstellen:
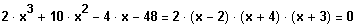
L = { 2 ; -4 ; -3 }
Am Beispiel: Löse
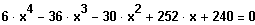
1. Schritt: Versuche eine Lösung zu erhalten: Graph zeichnen, probieren
Eine Lösung könnte -1 sein
-1 in die Funktionsgleichung einsetzen:
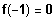Also ist -1 eine Lösung
Umformung:
----->
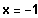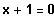
Wenn -1 eine Lösung ist, steckt der Linearfaktor
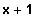im Funktionsterm.
2. Schritt: Der Linearfaktor wird abdividiert, das vereinfacht die Gleichung um einen Grad.
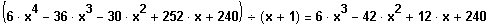
3. Schritt: Wie 1. Schritt. Versuche eine Lösung der vereinfachten Gleichung zu erhalten: Graph zeichnen, probieren
Eine Lösung könnte -2 sein
-2 in die Funktionsgleichung einsetzen:
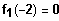Also ist -2 eine Lösung
Umformung:
----->
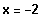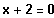
Wenn -2 eine Lösung ist, steckt der Linearfaktor
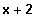im Funktionsterm.
4. Schritt: Der Linearfaktor wird abdividiert, das vereinfacht die Gleichung um einen Grad.
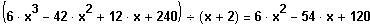
5. Schritt: Die quadratische Gleichung wird gelöst.
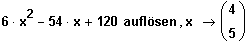
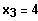und
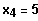
Die Polynomgleichung lässt sich als linearfaktorzerlegt darstellen:
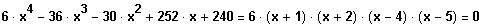
L = { -1 ; -2 ; 4 ; 5 }
