MK 25.6.2004 GrenzwertMA.mcd
Musteraufgaben zur Grenzwertbestimmung
Aufgaben:
(1)
Gegeben ist die Funktion
.
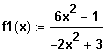Ab welchem Wert r weicht für alle r < x der Funktionswert f1(x) höchstens
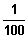vom Wert -3 ab?
(2)
Gegeben ist die Funktion
.
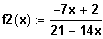Vermuten Sie einen Grenzwert a der Funktionswerte für x -->
.
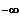Ab welchem Wert l weicht für alle x < l der Funktionswert f2(x) höchstens
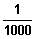von Ihrem Wert a ab?
(3)
Gegeben ist die Funktion
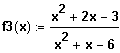in ihrer maximaler Definitionsmenge.
Untersuchen Sie das Verhalten der Funktionswerte in der Nähe der Definitinslücken.
für
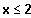
(4)
Gegeben sei die zusammengesetzte Funktion
=
{
für
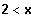
Untersuchen Sie das Verhalten der Funktionswerte an der Nahtstelle.
Lösungen:
(1)
Gegeben ist die Funktion
.
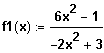Ab welchem Wert r weicht für alle r < x der Funktionswert f1(x) höchstens
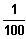vom Wert -3 ab?
x -- >
:
=>
=>
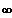Sei
=>
=>
=>
=>
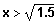
Für alle
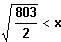ist
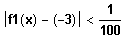
(2)
Gegeben ist die Funktion
.
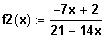Vermuten Sie einen Grenzwert a der Funktionswerte für x -->
.
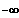Ab welchem Wert l weicht für alle x < l der Funktionswert f2(x) höchstens
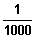von Ihrem Wert a ab?
x -->
----------------------->
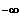
also
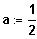
x -- >
:
=>
=>
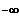Sei
=>
=>
=>
=>
=>
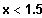
Für alle
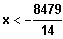ist
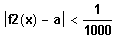
(3)
Gegeben ist die Funktion
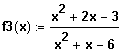in ihrer maximaler Definitionsmenge.
Untersuchen Sie das Verhalten der Funktionswerte in der Nähe der Definitinslücken.
Zuerst wird die Definitionsmenge (also die Definitionslücken) bestimmt:
=> D = R \ { -3 ; 2 }
Dann werden die Lücken der Reihe nach untersucht:
LS:
=
RS:
=
Rechtsseitiger und linksseitiger Grenzwert
an der Stelle -3 existieren und stimmen überein
Die Funktionswerte von f3(x)
konvergieren gegen den
Grenzwert
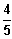für x--> -3
=>
An der Stelle x1 = -3 gibt es eine hebbare Definitionslücke
LS:
---> 5
=
--->
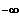
=> f3(x) ist divergent für x --> 2
--->
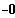
RS:
---> 5
=
--->
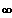
=> f3(x) ist divergent für x --> 2
---> +0
An der Stelle x2 = 2 gibt es eine Unendlichkeitsstelle (Polstelle) mit Vorzeichenwechsel
für
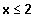
(4)
Gegeben sei die zusammengesetzte Funktion
=
{
für
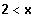
Untersuchen Sie das Verhalten der Funktionswerte an der Nahtstelle.
LS:
RS:
Rechtsseitiger und linksseitiger Grenzwert an der Stelle 2 existieren aber stimmen nicht überein.
=> Es gibt keinen Grenzwert an der an der Stelle 2.
An der Stelle x = 2 gibt es einen Sprung
