MK 3.6.2003 Grenzwert_e.mcd
Die Eulersche Zahl als Grenzwert
Herr Hyronimus Hurtig hat 1000€ übrig. Er möchte sein Geld arbeitenlassen und seinen Urenkeln ein sorgenfreies Leben ermöglichen. Er will sein Kapital auf 100 Jahre binden.
Dazu holt er Angebote von verschiedenen Banken ein.
Alle Banken bieten im Prinzip den gleichen Jahreszinssatz an, 1% im Jahr.
Das Bankhaus Raffzahn&Gierig bietet 100% pro 100Jahre, einmal verzinst. (Man denkt langfristig)
Die Öko-Alternativ-Bank bietet 10% pro 10Jahre, zehnmal verzinst.
Die Privatbank Schneider-Geier bietet 1% pro Jahr, also wird 100 Mal verzinst.
Wir berechnen Hurtigs Gewinn. Sei
Bankhaus Raffzahn&Gierig:
Die Öko-Alternativ-Bank:
usw.
Besser:
Wir sind Mathematiker, keine Banker. Also wollen wir bei der Berechnung etwas methodischer vorgehen:
Gegeben: (z.B.)
Allgemein:
Noch besser:
"Zinseszins"
Hiermit lässt sich die Privatbank Schneider-Geier leicht berechnen:
Noch einmal alle im direkten Vergleich:
Bankhaus Raffzahn&Gierig:
Verdoppelt!
Die Öko-Alternativ-Bank:
Ver-2.6-facht!
Die Privatbank Schneider-Geier:
Ver-2.7-facht!
wobei hier zufällig immer gilt
Letzlich gilt also
Aufgabe:
Unser Herr Hyronimus Hurtig ist höchst interessiert an der Klärung einiger brennender Fragen.
(1) Die Bank Lab- und Mühsal bietet eine monatliche Verzinsung zu 1/12%. Die Bank ist aber 100 km weit vom Wohnort von Hyronimus Hurtig entfernt beheimatet. Lohnt sich das?
(2) Würde es sich lohnen, wenn Herr Hurtig eine tägliche Verzinsung von 1/365% verhandeln kann?
(3) Was geschieht, wenn die Verzinsungszeiträume immer kürzer werden?
(Motto: "Wir verzinsen im Millisekundenintervall")
(4) Gibt es letzlich eine Obergrenze für den Term
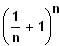, wenn n immer größer wird?
Helfen Sie Herrn Hyronimus Hurtig.
Berechnen Sie einige weitere Angebote, wie z.B. oben angegeben und beurteilen Sie die Ergebnisse im Sinne von Herrn Hyronimus Hurtig.
Zeichnen Sie den Graphen der Funktion
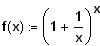mit vernünftigen Werten in ein Koordinatensystem und erklären Sie Herrn Hurtig die Tragweite Ihres Ergebnisses.
Lösungen:
Die Privatbank Schneider-Geier:
Die Bank Lab- und Mühsal:
Das macht einen Unterschied von ca. 12,30€.
mit Verhandlungsgeschick:
Das macht einen Unterschied von ca. 13,40€.
Dafür fährt man keine 100 km weit.
Wenn die Verzinsungszeiträume kürzer werden, steigt die Endsumme weiter an.
Der Anstieg wird aber augenscheinlich immer geringer.
Hier scheint eine absolute, obere Grenze zu bestehen.
Tatsächlich ist der "Grenzwert" des Ausdrucks
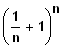für beliebig große n eine Naturkonstante,
die Eulersche Zahl e.
Die Eulersche Zahl e ist eine irrationale Zahl (nicht abbrechende, nicht periodische Dezimalzahl) wie auch p.
(auf 15 Stellen genau)
