MK 2.8.2003Grenzwert_gegen_x0.mcd
Nach Lehrplan ist die e-d-Methode
nicht zwingend vorgeschrieben
Grenzwerte gegen einen festen Wert x0
Bsp.:
D = R \ { 0 }
Die Funktion hat an der Stelle x = 0 eine
Definitionslücke.
Welche Werte nimmt die Funktion unmittelbar
daneben an?
Die Funktion nähert sich dem
Wert y =1 beliebig nahe
für x --> 0
Es gilt
mit D = R \ { 0 }
Für ein beliebiges e>0
gilt:
=>
Also gilt für alle x
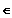Ue/2(0)
ohne 0 selbst:
Def.:
Unter einer punktierten s - Umgebung einer Zahl x0
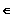R
versteht man für ein beliebiges
s
> 0 die Menge U*e(x0)
= Ue(x0)
\ { x0 }
Def.:
Eine Funktion y = f(x) mit x
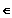D, die für jedes s
> 0 mit U*s(x0)
eine nicht leere Menge U*s(x0)
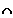D
besitzt, konvergiert für x -> x0 gegen den
Grenzwert a,
wenn sich zu jedem e
> 0 eine reelle Zahl d
> 0 so bestimmen lässt, dass
für x
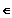U*d(x0)
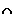D
gilt f (x)
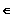Ue(a)
Schreibweise:
