MK 3.6.2003 Grenzwertexgegenunend.mcd
Einführung des Grenzwertes
Grenzwerte einer Funktion für x->
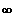am Beispiel
D = R+
Ab einem bestimmten x-Wert liegen alle y-Werte
unterhalb eines angenommenen y-Wertes
Bsp: Obergrenze 2
ab ca. x = 2 liegen alle Funktionswerte zwischen 1 und 2
Bsp: Obergrenze 1.3
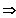ab ca. x = 8 liegen alle Funktionswerte zwischen 1 und 1.3
Also nähert sich wahrscheinlich der
Funktionswert der Zahl 1 beliebig, wenn x ->
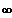
Definition
des Grenzwertes
Grenzwert der Funktion
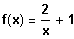existiere , falls man sich von oben (y- Wert)
beliebig unserem vermuteten Grenzwert 1
nähern kann und trotzdem einen Wert xr
für die x-Werte bestimmen kann so dass
für alle weiter rechts (von xr) liegenden
Werte immer unterhalb unserer angenommenen oberen
Schranke liegen.
Allgemein:
Eine Funktion f(x) mit rechtsseitig
unbeschränkter Definitionsmenge D konvergiert gegen den
Grenzwert a, falls
es zu jedem e > 0
eine Zahl r gibt, so dass für alle x > r
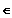D gilt:
f(x)
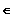Ue(a).
Unter der e-Umgebung
einer Zahl versteht man die Menge
Ue(a) = { t
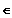R | a - e
< t < a + e }
= ] a - e
; a + e [
=
{ t
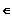R | |t - a| < e }
Das Bsp. von oben:
Funktion
vermuteter Grenzwert a = 1
Gegeben: e
Gesucht: r
=>
Bsp.: Sei
Dann ist
Also: Für x > 2000 gilt | f(x) - 1| <
0.001
