MK 4.6.2003 Extremwerte.mcd

Extremwerte

Def.:

f sei stetig. f hat an der Stelle x0 ein relatives Extremum, wenn gilt:

f(x0 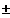h) < f(x0) "relatives Maximum"
mit h>0
f(x0 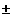h) > f(x0) "relatives Minimum"

Diese Definition lässt praktisches Rechnen kaum zu. Abhilfe?

Ein Wanderer geht ein Stück bergauf, dann hat er einen Moment keinen Anstieg mehr, dann gehts bergab.
Wo war der Wanderer gerade?

Ein Radler fährt ohne zu treten hinab, dann hat er einen Moment kein Gefälle mehr, dann muss er tüchtig in die Pedale steigen. Durch welchen Punkt ist er gerade gekommen?

Maximum:

Minimum:

steigen fallen
f ' (x) >0 f ' (x)<0

fallen steigen
f ' (x) < 0 f ' (x) >0

Daraus kann man folgenden Satz erhalten:

Satz:

f sei differenzierbar.

f hat an der Stelle x0 ein relatives Maximum, wenn gilt: f ' (x0 - h) > 0 und f ' (x0 + h) < 0
mit h>0
f hat an der Stelle x0 ein relatives Minimum, wenn gilt: f ' (x0 - h) < 0 und f ' (x0 + h) > 0

Also: VZW der ersten Ableitung von + auf - : Maximum an dieser Stelle
VZW der ersten Ableitung von - auf + : Minimum an dieser Stelle

Bsp.:

x0 = -2

> 0, steigen

relatives Maximum

< 0, fallen

x0 = 1

< 0, fallen

relatives Minimum

> 0, steigen

steigen                fallen               steigen

relatives Maximum

relatives Minimum

Impressum · Datenschutz