MK 2.2.2009 MonoEx_Ueb2.mcd
Übung: Monotonie und Extrempunkte mit Parameter
Aufgabe:
Bestimmen Sie in Abhängigkeit vom reellen Parameter k die Stellen mit den waagrechten Tangenten.
(1a)
(1b)
(1c)
(1d)
(2)
Bestimmen Sie in Abhängigkeit vom reellen Parameter c die maximalen Monotonieintervalle und Extrempunkte, machen Sie eine Skizze für c = 1.
(3)
Bestimmen Sie in Abhängigkeit vom reellen Parameter p die maximalen Monotonieintervalle und die Extrempunkte.
(4)
Bestimmen Sie den reellen Parameter q so, dass die Funktion f4 an der Stelle x = 2 ein Extremum besitzt. Berechnen Sie dann die maximalen Monotonieintervalle und die Extrempunkte.
(5)
Berechnen Sie den Parameter u so, dass Funktion f5 symmetrisch wird. Berechnen Sie dann die maximalen Monotonieintervalle und die Extrempunkte. Bestimmen Sie die Gleichungen aller Tangenten, die auf der Geraden
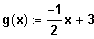 senkrecht stehen.
senkrecht stehen.
Lösungen:
Bestimmen Sie in Abhängigkeit vom reellen Parameter k die Stellen mit den waagrechten Tangenten.
(1a)
(1b)
(1c)
(1d)
(2)
Bestimmen Sie in Abhängigkeit vom reellen Parameter c die maximalen Monotonieintervalle und Extrempunkte, machen Sie eine Skizze für c = 1.
1. Fall:
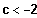
steigen
fallen
steigen
Maximum
Minimum
f2 ist streng monoton zunehmend für
oder
f2 ist streng monoton abnehmend für
Maximum bei x = c
Minimum bei x = -2
2. Fall:
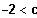
steigen
fallen
steigen
Maximum
Minimum
f2 ist streng monoton zunehmend für
oder
f2 ist streng monoton abnehmend für
Maximum bei x = -2
Minimum bei x = c
3. Fall:
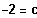
f2 ist streng monoton zunehmend in ganz R, es gibt keine Extrempunkte
(3)
Bestimmen Sie in Abhängigkeit vom reellen Parameter p die maximalen Monotonieintervalle und die Extrempunkte.
1. Fall:
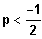
4. Fall:
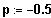
steigen
fallen
steigen
Maximum
Minimum
nix
2. Fall:
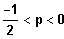
nur steigen
5. Fall:
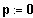
steigen
fallen
steigen
Maximum
Minimum
nix
2. Fall:
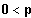
steigen
fallen
steigen
Maximum
Minimum
steigen
fallen
fallen
steigen
Maximum
nix
Minimum
(4)
Bestimmen Sie den reellen Parameter q so, dass die Funktion f4 an der Stelle x = 2 ein Extremum besitzt. Berechnen Sie dann die maximalen Monotonieintervalle und die Extrempunkte.
1. Fall:
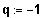
fallen
steigen
fallen
steigen
Minimum
Maximum
Minimum
2. Fall:
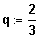
fallen
steigen
fallen
steigen
Minimum
Maximum
Minimum
(5)
Berechnen Sie den Parameter u so, dass Funktion f5 symmetrisch wird. Berechnen Sie dann die maximalen Monotonieintervalle und die Extrempunkte. Bestimmen Sie die Gleichungen aller Tangenten, die auf der Geraden
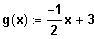 senkrecht stehen.
senkrecht stehen.
punktsymmetrisch zun Ursprung
steigen
fallen
steigen
fallen
steigen
Maximum
Minimum
Maximum
Minimum
senkrecht zu g:
=>
=>
=>