GS - 24.08.04 - abl_08_Monotonie.mcd
Monotonie und maximale Monotonieintervalle
- Krümmung und maximale Krümmungsintervalle -
Definition der Monotonie:
Gf ist streng monoton steigend, falls
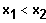
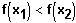
Gf ist streng monoton fallend, falls
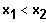
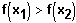
Für stetige, differenzierbare und auf einem zusammenhängenden Intervall definierte Funktionen ist
folgendes Kriterium eine hinreichende Bedingung:
Kriterium der Monotonie:
Gf ist streng monoton steigend, falls
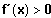
Gf ist streng monoton fallend, falls
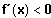
Quelle: Bronstein/Semendjajew, Taschenbuch der Mathematik, Verlag Harri Deutsch Frankfurt
Definition der Krümmung:
Unter der Krümmung einer Funktion f versteht man die "Steigung der Steigung".
Die Funktion f heißt linksgekrümmt (lk), wenn die Steigung der Tangente zunimmt.
Die Funktion f heißt rechtsgekrümmt (rk), wenn die Steigung der Tangente abnimmt.
Kriterium für das Krümmungsverhalten:
Die Funktion f heißt linksgekrümmt (lk)
f´´(x) > 0
Die Funktion f heißt rechtsgekrümmt (rk)
f´´(x) < 0
Beispiel 1:
Definitionsmenge: ID = IR
1. Ableitung:
Gf
lk
Gf '
x0 = 0
f'(x) - +
Gf smofa smost
Interpretation: TP aaa
Angabe der Monotoniebereiche:
Gf ist streng monoton fallend für x
]
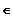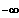; 0 ] und Gf ist streng monoton steigend für x
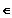[ 0 ;
[
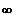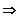Das Extremum ist ein relatives Minimum: TP (0/0)
Bemerkung:
Die Stelle
(horizontale Tangente) am Rand des Monotonieintervalls ist dabei, denn die definierende Eigenschaft ist erfüllt.
Das Kriterium funktioniert auch, wenn für eine (oder mehrere) einzelne Stellen innerhalb des Intervalls gilt:
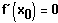(siehe Beispiel 2)
2. Ableitung:
ist immer positiv
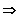Gf ist linksgekrümmt auf IR.
Beispiel 2:
Funktion:
Definitionsmenge: ID = IR
dreifache Nullstelle:
NS1,2,3( 0 / 0 )
1. Ableitung:
2. Ableitung:
Es gilt:
falls
und:
Eine zweifache Nullstelle der 1. Ableitung bedeutet, dass sich die Monotonieeigenschaft nicht
ändert.
f(x2)
Gf
lk
G f '
x1
x2
x0 = 0
f'(x) > 0 f'(x0) = 0 f'(x) > 0
rk
Gf smofa hor. Tang smost
f(x1)
Interpretation: Terrassenpunkt
Monotoniebereich: Gf ist streng monoton steigend in IR.
Bemerkung:
Die Anwendung des Monotonie-Kriteriums ist erlaubt, da fx (0) = 0 nur an einer einzelnen Stelle x0
(dürfen auch mehrere sein, sofern sie nicht nebeneinander liegen) gilt.
Die definierende Eigenschaft der Monotonie ist erfüllt, denn:
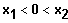
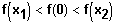
Vorzeichen der 2. Ableitung:
Krümmungsbereiche:
Gf ist rechtsgekrümmt für ]
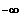; 0] und Gf ist linksgekrümmt für [ 0 ;
[.
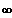Beispiel 3:
1. Ableitung:
Horizontale Tangenten:
2. Ableitung:
Vorzeichen der 2. Ableitung:
WP ( 2 / 0,77)
Vorzeichen der 1. Ableitung
Gf '
Vorzeichen: + - +
f'(x) + - +
Gf smost smofa smost
Interpretation: HP TP
Monotoniebereiche:
Gf ist streng mon. steigend für x
]
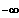; 2 ] und
Gf ist streng mon. fallend für x
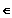[ 2 ; 6 ] und
Gf ist streng mon. steigend für x
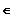[ 6 ;
[
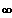Krümmungsbereiche:
Gf ist rechtsgekrümmt für x
]
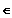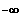; 4 ] und Gf ist linksgekrümmt für x
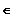[ 4 ;
[
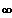Gf
rk
WP
lk
Beispiel 4:
Gf
Funktion:
lk
Definitionsmenge: ID = IR \ {0}
1. Ableitung:
Gf
ist überall negativ
rk
2. Ableitung:
Monotoniebereiche:
Falsch:
Gf ist streng monoton fallend in ID = IR \ {0}
(durchlöchertes Intervall)
Falsch:
Gf ist streng monoton fallend in x
]
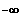; 0 [
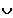] 0 ; +
[
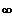(nicht zusammenhängendes Intervall)
Richtig:
Gf ist streng monoton fallend für x
]
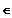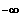; 0 [ und
Gf ist streng monoton fallend für ] 0 ; +
[
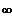Andere Schreibweise:
Gf streng monoton fallend
{ x l
}
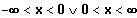Andere Schreibweise:
Gf streng monoton fallend
{
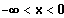} und {
}
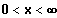Krümmungsbereiche:
Gf ist rechtsgekrümmt für x
]
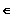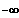; 0 [ und
Gf ist linksgekrümmt für ] 0 ; +
[
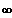Beispiel 5:
Funktion:
Partialbruchzerlegung:
schiefe Asymptote:
Definitionsmenge: ID = IR \ {1}
Nullstellen:
1. Ableitung:
Faktorisiert:
Zähler:
Horizontale Tangenten:
Ableitung positiv:
Ableitung negativ:
Nenner:
immer positiv
Gf
lk
TP
A2
HP
rk
Gf
A1: x0 = 1
Monotoniebereiche:
Gf ist streng monoton steigend in x
]
;
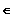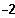[ und in x
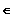] 4 ; +
[ und
Gf ist streng monoton fallend in x
[
;
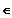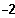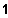[ und in x
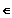] 1 ; 4 [
Krümmungsbereiche:
Gf ist rechtsgekrümmt in x
]
;
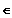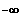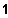[ und Gf ist linksgekrümmt in x
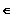] 1 ; +
[
Monotoniebereiche:
Graphische Lösung Variante 1:
Gz
Zähler + - - +
-2
4
Nenner + + + +
f '(x) + - - +
Gf smost smofa smofa smost
Interpretation: HP Pol TP
Graphische Lösung Variante 2:
x + 2 - + + +
x - 4 - - - +
- 2
4
(x-1)2 + + + +
f '(x) + - - +
Gf smost smofa smofa smost
Interpretation: HP Pol TP
