MK 31.3.2008 Parabel_Gerade_Dreieck .mcd
Die Optimierung einer Fläche
1. Eine ganzrationale Funktion 2. Grades hat ihr Minimum im Punkt (
/
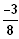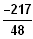) geht durch den Punkt (
/
).
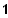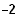Bestimmen Sie die Funktionsgleichung.
[ Ergebnis:
]
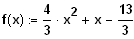2. Die Gerade g, eine Normale zur Geraden n:
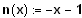, hat mit n die Nullstelle gemeinsam.
Bestimmen Sie die Funktionsgleichung.
[ Ergebnis:
]
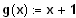3. Skizzieren Sie die Graphen von f und g in ein Koordinatensystem.
4. Die Graphen von f und g umschließen ein Flächenstück. Berechnen Sie den Flächeninhalt.
5.0 Die Schnittpunkte zwischen f und g (A und B), sowie ein Punkt P (auf dem Stück des Graphen von f, das zwischen A und B verläuft) bilden ein Dreieck.
5.1 Geben Sie eine sinnvolle Definitionsmenge für die x-Koordinate von P an.
5.2 Ein möglicher Punkt P ist (
/
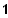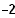). Skizzieren Sie für diesen Punkt P das Dreick ABP in das vorhandene Koordinatensystem und berechnen Sie den Flächeninhalt dieses Dreiecks.
5.3 Wie groß wird der Flächeninhalt, falls P --> A oder P --> B ?
5.4 Der Flächeninhalt des Dreiecks muss also maximal werden, wenn sich P irgendwo zwischen A und B befindet. Probieren Sie mit Geonext aus, wo sich P befinden muss und wie groß etwa der maximale Flächeninhalt ist.
Musterlösung:
1. Eine ganzrationale Funktion 2. Grades hat ihr Minimum im Punkt (
/
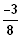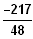) geht durch den Punkt (
/
).
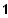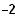Bestimmen Sie die Funktionsgleichung.
[ Ergebnis:
]
I
II
III
II-III:
IV
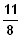* I + IV:
=>
in I:
=>
in III:
=>
=>
2. Die Gerade g, eine Normale zur Geraden n:
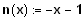, hat mit n die Nullstelle gemeinsam.
Bestimmen Sie die Funktionsgleichung.
[ Ergebnis:
]
=>
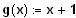Nullstelle:
=>
g:
=>
=>
3. Skizzieren Sie die Graphen von f und g in ein Koordinatensystem.
4. Die Graphen von f und g umschließen ein Flächenstück. Berechnen Sie den Flächeninhalt.
Schneide g und f:
=>
"+C"
A = [
]
=
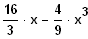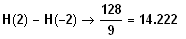
5.0 Die Schnittpunkte zwischen f und g (A und B), sowie ein Punkt P (auf dem Stück des Graphen von f, das zwischen A und B verläuft) bilden ein Dreieck.
5.1 Geben Sie eine sinnvolle Definitionsmenge für die x-Koordinate von P an.
5.2 Ein möglicher Punkt P ist (
/
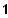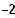). Skizzieren Sie für diesen Punkt P das Dreick ABP in das vorhandene Koordinatensystem und berechnen Sie den Flächeninhalt dieses Dreiecks.
Defintionsmenge:
xP
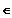] -2 ; 2 [
Strecke AB:
Höhe des Dreiecks:
Lot von P auf g => Lotfußpunkt ( -1 / 0)
5.3 Wie groß wird der Flächeninhalt, falls P --> A oder P --> B ?
Fläche( P --> A ) -----> 0
Fläche( P --> B ) -----> 0
Das Dreieck hat dann keine Höhe mehr!
5.4 Der Flächeninhalt des Dreiecks muss also maximal werden, wenn sich P irgendwo zwischen A und B befindet. Probieren Sie mit Geonext aus, wo sich P befinden muss und wie groß etwa der maximale Flächeninhalt ist.
5.5 Finden Sie den Punkt P und berechnen Sie den maximal möglichen Flächeninhalt. (Das ist nicht einfach!)
1. Möglichkeit: (Mit den Mitteln der Differentialrechnung)
Normale np zu g durch P(xp / f(xp)):
Schneide np und g:
in np:
das gibt den Lotfußpunkt: (
/
)
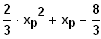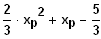Also wird die Höhe im Dreieck:
=
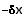
Mit AB ergibt sich die Fläche:
Wir suchen ein Maximum davon:
=>
< 0 => Maximum!
Also P( 0 /
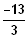) und
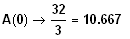
2. Möglichkeit: (Durch heftiges Nachdenken!)
Die Seite AB bleibt für alle Punkte P gleich. Also ist es nur die Höhe, auf die es ankommt. Gesucht ist die größe Höhe. Man findet diese Höhe, indem man eine Parallele zu g der Kurve von f nähert, bis sie den Graph von f berührt. (Mit Geonext ausprobieren!) Gesucht ist dann letztlich ein Punkt P, der eine Tangente mit der gleichen Steigung wie g aufweist.
=>
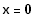
(Pythagoras)
