MK 4.6.2003 DefStetigkeit.mcd
Definition der Stetigkeit
Def.: Eine Funktion y = f(x) mit D = [
a;b ] heißt stetig an der Stelle x0
€ ] a;b[ , wenn gilt:
Die Funktion f heißt stetig in einem
Intervall, wenn sie an jeder Stelle des Intervalls stetig ist.
Bemerkung:
Da für die Stetigkeit der Wert f(x0)
existieren muss, kann nur für Werte aus der Definitionsmenge eine
Aussage über Stetigkeit gemacht werden.
Da am Rand einer Definitionsmenge jeweils der
linksseitige oder rechtsseitige Grenzwert nicht bestimmbar ist, spricht
man am Rand von einseitiger Stetigkeit, wenn der bestimmbare Grenzwert
und der Funktionswert übereinstimmen.
Insgesamt heißt eine Funktion stetig im
Definitionsbereich, wenn sie am Rand einseitig stetig und sonst
überall stetig ist.
Bsp.:
(1)
ist stetig in R
(2)
ist stetig in R
Es gilt
Also ist f stetig an der Stelle x0. Wenn x0 nun
beliebig aus R war, gilt
genauso f ist stetig in ganz R.
(3)
ist stetig in R
(4)
ist stetig in R
(5)
ist stetig in R+0
( Stetig in ] 0;
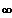 [,
einseitig stetig bei 0 )
[,
einseitig stetig bei 0 )
Satz:
Die Funktionen f und g seien stetig in einem
Intervall. Dann ist auch h = f + - * /
g stetig.
Für / muss
gelten
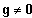
Zum Beweis kann man die Grenzwertsätze
verwenden.
Polynomfunktionen lassen sich mit den Operationen + - * und Konstanten und der Funktion
f(x) = x bilden.
Folgerung: Polynomfunktionen sind stetig in R
Gebrochen-rationale Funktionen werden gebildet
Polynomfunktion /
Polynomfunktion.
Folgerung: Gebrochen-rationale Funktionen
sind stetig in R \ { Nennernullstellen }
Stetigkeit anschaulich: Eine Funktion ist stetig, wenn
sich ihr Graph ohne abzusetzen zeichnen lässt.