MK 5.7.2004 DeflueckenMA.mcd
Musteraufgaben zu Definitionslücken
(1)
Gegeben sei die Funktion
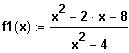 .
.
(1.1) Bestimmen Sie die Definitionsmenge.
(1.2) Bestimmen Sie das Verhalten der
Funktionswerte an den Defintionslücken.
(1.3) Bestimmen Sie die Nullstellen.
(1.4) Wie könnte man bei diesem Funktionstyp
also hebbare und nicht behebbare
Definitionslücken bestimmen?
(2)
Gegeben sei die Funktion
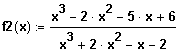 .
.
(2.1) Bestimmen Sie die Definitionsmenge.
(2.2) Bestimmen Sie die Nullstellen.
(2.3) Kürzen Sie den Funktionsterm soweit wie
möglich.
(2.4) Welche Defintionslücken sind hebbar,
welche nicht?
(2.5) Beheben Sie die Definitionslücken durch
zusätzliche Definition.
für x
< 1
(3)
Betrachten Sie die Funktion f3(x)=
{
für
mit k € R
(3.1) Bestimmen Sie die Definitionsmenge.
(3.2) Bestimmen Sie das Verhalten der
Funktionswerte an den Definitionslücken.
(3.3) Probieren Sie mit Geonext den Parameter k so
zu bestimmen, dass an der Nahtstelle der Übergang
stetig wird.
(3.4) Weisen Sie die Stetigkeit für ihre
Schätzung nach.
Lösungen:
(1)
Gegeben sei die Funktion
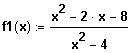 .
.
(1.1) Bestimmen Sie die Definitionsmenge.
(1.2) Bestimmen Sie das Verhalten der
Funktionswerte an den Defintionslücken.
(1.3) Bestimmen Sie die Nullstellen.
(1.4) Wie könnte man bei diesem Funktionstyp
also hebbare und nicht behebbare
Definitionslücken bestimmen?
=> D = R \ { -2 ; 2 }
LS:
=
RS:
=>
Es handelt sich um eine hebbare
Definitionslücke.
LS:
=
RS:
=> Es handelt sich hier um eine nicht hebbare
Definitionslücke, um eine Unendlichkeitsstelle (Polstelle)
mit Vorzeichenwechsel.
Es gibt eine Nullstelle bei 4, einen Schnittpunkt
Die zweite Lösung, -2, ist keine Nullstelle,
siehe D.
Offensichtlich heben sich Zählernullstelle
und Nennernullstelle auf. Man könnte also von der
Linearfaktorzerlegung der Funktion ausgehend soweit als möglich
kürzen. Was als Nennernulstelle übrigbleibt, ergibt nicht
hebbare Defintionslücken. Was als Nennernullstelle gekürzt
wurde, ist hebbare Defintionlücke.
(2)
Gegeben sei die Funktion
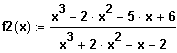 .
.
(2.1) Bestimmen Sie die Definitionsmenge.
(2.2) Bestimmen Sie die Nullstellen.
(2.3) Kürzen Sie den Funktionsterm soweit wie
möglich.
(2.4) Welche Defintionslücken sind hebbar,
welche nicht?
(2.5) Beheben Sie die Definitionslücken durch
zusätzliche Definition.
Finde
Poldiv:
=> D = R \ { -2 ; -1 ; 1 }
Finde
Poldiv:
=> L = { -2 ; 1 ; 3 }
=> Es gibt einen SP bei x = 3
Es gibt eine Polstelle mit VZW bei x = -1
und hebbare Definitionslücken bei x = -2 und
x = 1
Man definiert die zusätzlichen Punkte ( -2 /
5 ) und ( 1 / -1 ).
f2(x) für x € R \ { -2 ; -1 ; 1 }
5 für x = -2
-1 für x = 1
fneu(x)
=
= fn(x) mit D = R \ { -1 }
{
}
für x
< 1
(3)
Betrachten Sie die Funktion f3(x)=
{
für
mit k € R
(3.1) Bestimmen Sie die Definitionsmenge.
(3.2) Bestimmen Sie das Verhalten der
Funktionswerte an den Definitionslücken.
(3.3) Probieren Sie mit Geonext den Parameter k so
zu bestimmen, dass an der Nahtstelle der Übergang
stetig wird.
(3.4) Weisen Sie die Stetigkeit für ihre
Schätzung nach.
D = R \ { -1 }
LS:
RS:
An der Stelle x = -1 ist eine Polstelle mit
Vorzeichenwechsel.
Schätze k = 2.5
LS:
RS:
=> mit k = 2.5 ist f3(x) an der Nahtstelle x =
1 stetig.