MK 4.6.2003 SaetzeStetigkeit.mcd
Sätze über stetige Funktionen
Satz von der Beschränktheit
Wenn eine Funktion f in einem Intervall [ a; b]
stetig ist, dann ist sie in diesem Intervall auch beschränkt:
Es gibt eine Zahl k
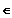 R
so, dass gilt
R
so, dass gilt
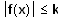 für
x
für
x
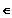 [ a;
b ]
[ a;
b ]
Bsp.:
mit D = [2;3] ist stetig und beschränkt.
mit D = ]0;3] ist stetig aber unbeschränkt
(Halboffenes Intervall!).
mit D = R \ {0} ist weder stetig in R noch
beschränkt in D.
Extremwertsatz
Wenn eine Funktion f in einem Intervall [ a; b]
stetig ist, dann hat sie in diesem Intervall auch einen kleinsten und
größten Wert.
<---- größter Wert
<---- kleinster Wert
Zwischenwertsatz
Eine in einem Intervall [ a; b] stetige Funktion f
mit den Funktionswerten f(a) und f(b) nimmt jeden Wert zwischen f(a)
und f(b) mindestens einmal an.
Nullstellensatz
Eine in einem Intervall [ a; b] stetige Funktion f
mit Funktionswerten f(a) und f(b) mit unterschiedlichem Vorzeichen,
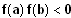 ,
hat in ] a; b [ mindestens eine Nullstelle.
,
hat in ] a; b [ mindestens eine Nullstelle.
<---- f(b) ist positiv
<---- f(a) ist negativ
Ein Beispiel:
Gegeben ist die Funktion
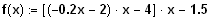 mit
der Definitionsmenge D = [ -8; 0.5 ],
mit
der Definitionsmenge D = [ -8; 0.5 ],
also
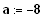 und
und
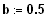 .
.
Aufgabe:
1. Ist f stetig in D ?
2. Ist f beschränkt ?
3. Ermitteln Sie mit dem Programm GEONExT
Schätzungen für einen absolut größten und kleinsten Wert.
4. Nach dem Zwischenwertsatz wird jeder Wert
zwischen f(a) und f(b) mindestens einmal angenommen.
Gibt es Werte, die mehrmals angenommen werden?
5. Gilt
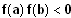 ?
Was bedeutet das?
?
Was bedeutet das?
6. Ermitteln Sie mit dem Programm GEONExT
Schätzungen für die Nullstellen.
7. Ermitteln Sie bessere Näherungen für die
Nullstellen mittels eines Bisektionsverfahrens mit einem
Tabellenkakulationsprogramm.
8. Ein Sekantenverfahren liefert schneller bessere
Näherungen. Realisieren Sie das in Mathcad.

Lösungen:
1. Ist f stetig in D ? Da f eine Polynomfunktion ist, ist f
stetig.
2. Ist f beschränkt ? Da f stetig ist, gilt der Satz von
der Beschränktheit.
3. Ermitteln Sie mit dem Programm GEONExT
Schätzungen für einen absolut größten und kleinsten Wert.
Kleinster
Wert ca. -6.7 größter Wert ca. +4.9
4. Nach dem Zwischenwertsatz wird jeder Wert
zwischen f(a) und f(b) mindestens einmal angenommen.
Gibt es Werte, die mehrmals angenommen werden?
5. Gilt
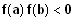 ? Was bedeutet das? Es existiert
mindestens eine Nullstelle in ] a; b [
? Was bedeutet das? Es existiert
mindestens eine Nullstelle in ] a; b [
6. Ermitteln Sie mit dem Programm GEONExT
Schätzungen für die Nullstellen.
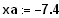
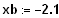
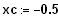
7. Ermitteln Sie bessere Näherungen für die
Nullstellen mittels eines Bisektionsverfahrens mit einem
Tabellenkakulationsprogramm.
Programmieren Sie Abfragen der Form
WENN( f(links)*f(mitte)>=0, mitte, links)
WENN( f(mitte)*f(rechts)>=0, mitte, rechts)
8. Ein Sekantenverfahren liefert schneller bessere
Näherungen. Realisieren Sie das in Mathcad.
Aus der Formelsammlung, S. 20 :
Aus der Formelsammlung, S. 20 :
Aus der Formelsammlung, S. 20 :
Und die Lösungen mit Mathcad dazu: