MK 4.6.2003 QuadUngleichungen.mcd
Quadratische Ungleichungen
Man kann quadratische Ungleichungen lösen,
indem man die zugehörige quadratische Funktion skizziert und so
bestimmen kann, bei welchen x-Werten sich der y-Wert unterhalb,
oberhalb oder auf der x-Achse befindet.
Bsp.:
Ungleichung:
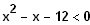
Zugehörige Funktion:
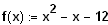
Die Funktion stellt eine nach oben geöffnete
Parabel dar.
Nullstellen:
Man findet zwei Nullstellen, bei
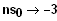 und
bei
und
bei
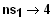 . Das
genügt, um die Funktion skizzieren zu können.
. Das
genügt, um die Funktion skizzieren zu können.
Jetzt kann man ablesen, dass x-Werte zwischen -3
und +4 negative y-Werte produzieren.
Es gilt: y =
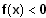 für x
für x
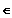 ] -3
; 4 [
] -3
; 4 [
also
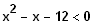 für x
für x
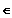 ] -3
; 4 [
] -3
; 4 [
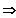 L = ]
-3 ; 4 [
L = ]
-3 ; 4 [
Bsp.:
Ungleichung:
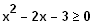
Zugehörige Funktion:
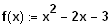
Die Funktion stellt eine nach oben geöffnete
Parabel dar.
Nullstellen:
Man findet zwei Nullstellen, bei
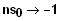 und
bei
und
bei
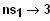 . Das
genügt, um die Funktion skizzieren zu können.
. Das
genügt, um die Funktion skizzieren zu können.
Jetzt kann man ablesen, dass x-Werte links von -1
(eingeschlossen) und rechts von +3 (eigeschlossen) positive (oder 0)
y-Werte produzieren.
Es gilt:
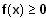 für x
für x
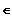 R \ ]
-1 ; 3 [
R \ ]
-1 ; 3 [
also
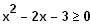 für x
für x
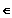 R \ ]
-1 ; 3 [
R \ ]
-1 ; 3 [
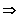 L = R
\ ] -1 ; 3 [
L = R
\ ] -1 ; 3 [