EL / GS - 23.08.05 - a2_linUngl.mcd
Lineare Ungleichungen
Definition:
Eine Ungleichung mit der Definitionsmenge ID
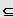G heißt linear (oder ersten Grades), wenn
sie in der Form
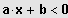bzw.
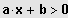mit a,b
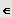IR und
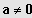darstellbar ist.
Bezeichnung: Ungleichungen, die die gleiche Lösungsmenge haben, heißen äquivalent.
Regeln:
Wird auf beiden Seiten einer Ungleichung derselbe Term addiert oder subtrahiert, so erhält
man eine äquivalente Ungleichung.
Werden beide Seiten mit demselben positiven Term multipliziert oder durch denselben positiven Term dividiert, so erhält man eine äquivalente Ungleichung.
Werden beide Seiten mit demselben negativen Term multipliziert oder durch denselben negativen Term dividiert, so muss man das Relationszeichen umdrehen (aus "<" wird ">"
und aus ">" wird "<"), um eine äquivalente Ungleichung zu erhalten.
Bestimmung der Lösungsmenge:
Sei
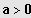
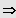
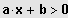
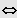
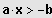
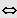
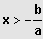IL = ]
;
[
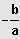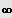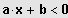
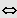
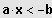
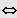
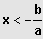IL = ]
;
[
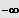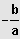Sei
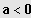
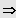
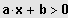
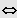
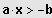
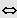
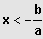IL = ]
;
[
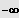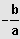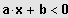
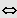
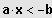
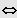
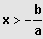IL = ]
;
[
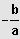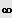Beispiele dazu siehe auf den nächsten Seiten.
Aufgabe 1:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR
Lösung:
IL = { x I
}
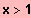Teilaufgabe b)
Darstellung der Ungleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Graphische Lösung der Ungleichung:
Aufgabe 2:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR
Lösung:
IL = { x I x ³ -1 }
Teilaufgabe b)
Darstellung der Ungleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Graphische Lösung der Ungleichung:
