EL / GS -23.08.05 - b2_quadUngl.mcd
Quadratische Ungleichungen
Definition:
Eine quadratische Ungleichung hat die Form
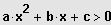 bzw.
bzw.
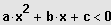
mit a, b, c
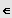 IR und
IR und
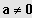 .
.
Bestimmung der Lösungsmenge:
(1) Bestimme die Lösungen x1 und x2 der Gleichung
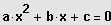 .
.
(2) Faktorisiere den quadratischen Term:
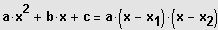
(3) Algebraische Lösung:
Das Produkt ist positiv, wenn beide Faktoren entweder positiv oder negativ sind.
Das Produkt ist negativ, wenn beide Faktoren verschiedenes Vorzeichen haben.
(4) Graphische Lösung:
Definiere einen Funktionsterm
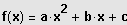 .
.
Suche die Nullstellen und faktorisiere damit den Funktionsterm
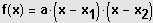 .
.
Zeichne den Graphen mit Hilfe der Nullstellen und der Kenntnis des Vorzeichens von a:
Für
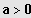 ist die Parabel nach oben geöffnet, für
ist die Parabel nach oben geöffnet, für
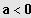 ist sie nach unten geöffnet.
ist sie nach unten geöffnet.
Die Ungleichung ist positiv, wenn der Graph oberhalb der x-Achse verläuft und sie ist
negativ, wenn der Graph unterhalb der x-Achse verläuft.
Bemerkung:
Eine quadr. Ungleichung der Form
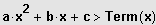 bzw.
bzw.
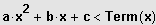
mit a, b, c
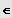 IR und
IR und
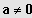 , wobei T(x) konstant, linear oder quadratisch sein kann, wird in die
, wobei T(x) konstant, linear oder quadratisch sein kann, wird in die
Normalform
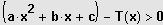 bzw.
bzw.
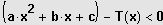 gebracht.
gebracht.
Beispiele dazu siehe auf den nächsten Seiten.
Aufgabe 1:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Ungleichung:
ID = IR
Gleichung:
Faktorisieren:
durch Faktorisierung, ergibt
Lösung:
IL = ]
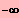 ; 2 [ È ] 4 ; ¥ [
; 2 [ È ] 4 ; ¥ [
Teilaufgabe b)
Parabel:
Frage: Wo verläuft der Graph oberhalb der x-Achse.
Nullstellen:
Die Parabel hat zwei einfache Nullstellen NS1(2 / 0) und NS2(4 / 0) und ist nach oben geöffnet.
Graphische Lösung der Unleichung:
Aufgabe 2:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
Ungleichung:
ID = IR
Gleichung:
Faktorisieren:
durch Faktorisierung, ergibt
Lösung:
IL = ] 2 ; 4 [
Teilaufgabe b)
Parabel:
Frage: Wo verläuft der Graph oberhalb der x-Achse.
Nullstellen:
Die Parabel hat zwei einfache Nullstellen NS1(2 / 0) und NS2(4 / 0) und ist nach unten geöffnet.
Graphische Lösung der Unleichung:
Aufgabe 3:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung einer geeigneten Funktion.
Teilaufgabe a)
ID = IR
Ungleichung:
Gleichung:
Faktorisieren:
durch Faktorisierung, ergibt
Lösung:
IL = ]
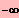 ; 2 ] È [ 3 ; ¥ [
; 2 ] È [ 3 ; ¥ [
Teilaufgabe b)
Parabel:
Frage: Wo schneidet der Graph die x-Achse bzw. wo verläuft er unterhalb?
Nullstellen:
Die Parabel hat zwei einfache Nullstellen NS1(2 / 0) und NS2(3 / 0) und ist nach unten geöffnet.
Graphische Lösung der Gleichung mit Unleichung:
Aufgabe 4:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR
Linke Seite:
Rechte Seite:
Normalform:
Lösungsmenge:
IL = ]
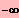 ; 0 [ È ] 2 ; ¥ [
; 0 [ È ] 2 ; ¥ [
Teilaufgabe b)
Darstellung der Ungleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Frage: Wo schneidet der Graph die x-Achse bzw. wo verläuft er unterhalb?
Bestimme diejenigen x-Werte, für die gilt:
Graphische Lösung der Ungleichung:
Aufgabe 5:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR
Linke Seite:
Rechte Seite:
Normalform:
Lösungsmenge:
IL = ]
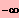 ; 1 [ È ] 3 ; ¥ [
; 1 [ È ] 3 ; ¥ [
Teilaufgabe b)
Darstellung der Ungleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Frage: Wo liegt die Parabel p über der Geraden g?
Bestimme diejenigen x-Werte, für die gilt:
Graphische Lösung der Ungleichung:
Aufgabe 6:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR
Linke Seite:
Rechte Seite:
Normalform:
Lösungsmenge:
IL = ]
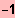 ; 1 [
; 1 [
Teilaufgabe b)
Darstellung der Ungleichung mit Funktionen:
Linke Funktion:
Rechte Funktion:
Differenzfunktion:
Frage: Wo sind die Funktionswerte der Parabel 1 unter denen der Parabel 2?
Bestimme diejenigen x-Werte, für die gilt:
Graphische Lösung der Ungleichung: