EL / GS - 23.08.05 - d2_Bruchungl.mcd
Bruchungleichungen
Bruchungleichungen (Standardform) werden gelöst nach dem Schema:
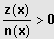
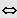
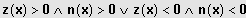"gleiches Vorzeichen"
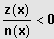
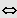
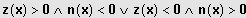"ungleiches Vorzeichen"
Allgemeine Bruchungleichung:
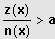
wird umgeformt:
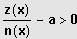
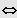
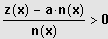
Standardform:
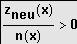Fallunterscheidung wie oben
Allgemeine Bruchungleichung:
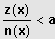
wird umgeformt:
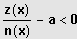
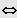
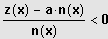
Standardform:
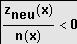Fallunterscheidung wie oben
Beispiele dazu siehe auf den nächsten Seiten.
Aufgabe 1:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR \ {-1}
Lösung:
IL = ]
;
[
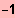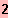Teilaufgabe b)
Zählerfunktion:
Nennerfunktion:
Funktionsterm:
Graphische Lösung der Ungleichung:
Aufgabe 2:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR \ {-1}
Lösung:
IL = ]
;
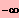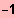[ È ] 2 ; ¥ [
Teilaufgabe b)
Zählerfunktion:
Nennerfunktion:
Funktionsterm:
Graphische Lösung der Ungleichung:
Aufgabe 3:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR \ {-1}
Lösung:
IL = ]
;
[
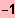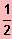Teilaufgabe b)
Standardform:
erweitert auf
Zählerfunktion:
Nennerfunktion:
Funktionsterm:
Graphische Lösung der Ungleichung:
Aufgabe 4:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR \ {-1}
Lösung:
Teilaufgabe b)
Standardform:
erweitert auf
Zählerfunktion:
Nennerfunktion:
Funktionsterm:
Graphische Lösung der Ungleichung:
Aufgabe 5:
a) Bestimmen Sie von der gegebenen Ungleichung die maximale Definitions- und die Lösungsmenge.
b) Veranschaulichen Sie die Ermittlung der Lösungsmenge mit Hilfe der graphischen Darstellung von
Funktionen
Teilaufgabe a)
Ungleichung:
ID = IR \ {-1; 1}
Umformungen:
vereinfacht auf
Standardform:
Lösung:
IL = ]-1; 1[
Teilaufgabe b)
Zählerfunktion:
Nennerfunktion:
Funktionsterm:
Graphische Lösung der Ungleichung:
