MK 4.6.2003 ArtenTerme.mcd
Arten von Termen
Ganzrationale Terme (Polynome):
Def.: Ein Polynom ist eine Summe von Produkten einer reellen Zahl mit Potenzen einer Variablen, wobei der Exponent aus N ist.
"Polynom vom Grade n"
Bsp.:
Polynom 4. Grades
Polynom 5. Grades
Rationale Terme:
Def.: Seien p(x) und q(x) ganzrationale Terme. Dann ist
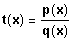ein rationaler Term.
Bsp.:
Erkenntnis: Ganzrationale Terme haben keine Einschränkung der Definitionsmenge, D = R, rationale Terme in der Regel schon (Die Nullstellen des Nenners).
Wurzeln:
Def.: Seien a € R0+ , n € N \{ 0 }. Dann ist
bestimmt durch
Bsp.:
Taschenrechner:
für x>=0
MERKE:
= {
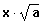für x<0
FEHLER:
RICHTIG:
keine Vereinfachung
möglich!
Wurzelterme:
Def.: Treten Variable als Bestandteil des Radikanden auf, so liegt ein Wurzelterm vor.
Bsp.:
